题目内容
在△ABC中,角A,B,C所对的边长分别为a,b,c,若△ABC的周长为
+1,且sinA+sinC=
sinB.
(1)求边长b;
(2)若△ABC的面积为
sinB,求角B的度数.
| 2 |
| 2 |
(1)求边长b;
(2)若△ABC的面积为
| 1 |
| 6 |
考点:正弦定理,余弦定理
专题:解三角形
分析:(1)由条件利用正弦定理可得 a+b+c=
+1,且a+c=
b,由此求得b的值.
(2)由△ABC的面积为
ac•sinB=
sinB,求得ac=
.再由余弦定理可得 cosB=
的值,即可求得角B的度数.
| 2 |
| 2 |
(2)由△ABC的面积为
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| (a+c)2-2ac-1 |
| 2ac |
解答:
解:(1)由条件利用正弦定理可得 a+b+c=
+1,且a+c=
b,
由此求得a+c=
,b=1.
(2)∵△ABC的面积为
ac•sinB=
sinB,∴ac=
.
再由余弦定理可得 cosB=
=
=
=
,
∴B=60°.
| 2 |
| 2 |
由此求得a+c=
| 2 |
(2)∵△ABC的面积为
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
再由余弦定理可得 cosB=
| a2+c2-b2 |
| 2ac |
| (a+c)2-2ac-1 |
| 2ac |
2-
| ||
2×
|
| 1 |
| 2 |
∴B=60°.
点评:本题主要考查正弦定理和余弦定理的应用,已知三角函数值求角的大小,属于基础题.

练习册系列答案
相关题目
 如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=2
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
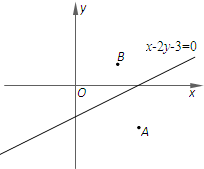 已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.
已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.