题目内容
已知直线l的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ2-4ρsinθ+2=0.
(Ⅰ)把圆C的极坐标方程化为直角坐标方程;
(Ⅱ)将直线l向右平移h个单位,所得直线l′与圆C相切,求h.
|
(Ⅰ)把圆C的极坐标方程化为直角坐标方程;
(Ⅱ)将直线l向右平移h个单位,所得直线l′与圆C相切,求h.
考点:简单曲线的极坐标方程,参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:(Ⅰ)利用ρ2=x2+y2,y=ρsinθ,可把圆C的极坐标方程化为直角坐标方程;
(Ⅱ)将直线l向右平移h个单位,所得直线l′
(t为参数),代入圆的方程,利用直线l′与圆C相切,建立方程,即可求h.
(Ⅱ)将直线l向右平移h个单位,所得直线l′
|
解答:
解:(Ⅰ)∵ρ2-4ρsinθ+2=0,
∴x2+y2-4y+2=0;
(Ⅱ)将直线l向右平移h个单位,所得直线l′
(t为参数),
代入圆的方程可得2t2+2(h-12)t+(h-10)2+2=0,
∵直线l′与圆C相切,
∴△=4(h-12)2-8[(h-10)2+2]=0,
即h2-16h+60=0,
∴h=6或h=10.
∴x2+y2-4y+2=0;
(Ⅱ)将直线l向右平移h个单位,所得直线l′
|
代入圆的方程可得2t2+2(h-12)t+(h-10)2+2=0,
∵直线l′与圆C相切,
∴△=4(h-12)2-8[(h-10)2+2]=0,
即h2-16h+60=0,
∴h=6或h=10.
点评:本题考查圆的参数方程与直线的极坐标方程与普通方程的互化,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知空间图形的三视图如图,空间几何体的表面积为( )
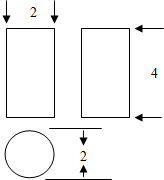

| A、8π | B、10π |
| C、12π | D、9π |
数列{an}的通项公式是an=
,前n项和为9,则n等于( )
| 1 | ||||
|
| A、9 | B、99 | C、10 | D、100 |