题目内容
曲线x2+y2=2与曲线y=x2所围成的区域的面积是多少?
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:将曲线x2+y2=2与曲线y=x2所围成的区域的面积分成两部分:弓形面积、直线y=1与与曲线y=x2所围成的区域的面积,利用定积分,即可求得结论.
解答:
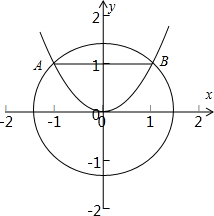 解:如图所示,由曲线x2+y2=2与曲线y=x2,可得A(-1,1),B(1,1),∴∠AOB=90°,
解:如图所示,由曲线x2+y2=2与曲线y=x2,可得A(-1,1),B(1,1),∴∠AOB=90°,
∴弓形面积为
π•2-
•2•1=
-1,
直线y=1与与曲线y=x2所围成的区域的面积是
(1-x2)dx
=(x-
x3)
=
.
∴曲线x2+y2=2与曲线y=x2所围成的区域的面积是
-1+
=
+
.
 解:如图所示,由曲线x2+y2=2与曲线y=x2,可得A(-1,1),B(1,1),∴∠AOB=90°,
解:如图所示,由曲线x2+y2=2与曲线y=x2,可得A(-1,1),B(1,1),∴∠AOB=90°,∴弓形面积为
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 2 |
直线y=1与与曲线y=x2所围成的区域的面积是
| ∫ | 1 -1 |
=(x-
| 1 |
| 3 |
| | | 1 -1 |
| 4 |
| 3 |
∴曲线x2+y2=2与曲线y=x2所围成的区域的面积是
| π |
| 2 |
| 4 |
| 3 |
| π |
| 2 |
| 1 |
| 3 |
点评:本题主要考查了定积分在求面积中的应用,以及定积分的计算,属于基础题.

练习册系列答案
相关题目
将函数图f(x)=sin(x-
)象上的所有点向左平移
个单位长度,则所得图象的函数解析式是( )
| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=cosx |
| C、y=-sinx |
| D、y=-cosx |
函数y=x|x|的图象经描点确定后的形状大致是( )
A、 |
B、 |
C、 |
D、 |
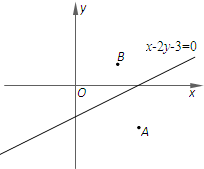 已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.
已知⊙P经过A(3,-2)、B(2,1)两点,圆心P在直线x-2y-3=0上.