题目内容
设不等式组
表示的平面区域为r,且函数y=logax的图象经过区域r,则实数a的取值范围是( )
|
A、(1,
| |||||
B、[
| |||||
C、[
| |||||
D、[
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据对数函数的图象和性质,即可得到结论.
解答:
 解:作出不等式组
解:作出不等式组
对应的平面区域如图:
若0<a<1,则由图象可知对数函数的图象一定与区域没有交点.
若a>1,当对数函数图象经过点A时,满足条件,
此时
,
解得
,即A(3,2),此时loga3=2,解得a=
,
当对数函数图象经过点B时,满足条件,
此时
,
解得
,即B(2,4),此时loga2=4,解得a=
,
∴实数a的取值范围是[
,
],
故选:C.
 解:作出不等式组
解:作出不等式组
|
若0<a<1,则由图象可知对数函数的图象一定与区域没有交点.
若a>1,当对数函数图象经过点A时,满足条件,
此时
|
解得
|
| 3 |
当对数函数图象经过点B时,满足条件,
此时
|
解得
|
| 4 | 2 |
∴实数a的取值范围是[
| 4 | 2 |
| 3 |
故选:C.
点评:本题主要考查线性规划的应用,利用对数函数的图象和性质,通过数形结合是解决本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
将函数图f(x)=sin(x-
)象上的所有点向左平移
个单位长度,则所得图象的函数解析式是( )
| π |
| 4 |
| π |
| 4 |
| A、y=sinx |
| B、y=cosx |
| C、y=-sinx |
| D、y=-cosx |
在直角坐标系和以原点为极点,以x轴正方向为极轴建立的极坐标系中,直线l:y+kx+2=0与曲线C:ρ=2cosθ相交,则k的取值范围是( )
| A、k∈R | ||
B、k≥-
| ||
C、k<-
| ||
| D、k∈R但k≠0 |
 如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=2
如图,在三棱锥S-ABC中,E为棱SC的中点,若AC=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
已知空间图形的三视图如图,空间几何体的表面积为( )
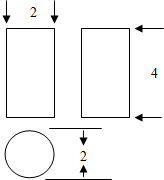

| A、8π | B、10π |
| C、12π | D、9π |