题目内容
16.定义在R上的函数f(x)在(6,+∞)上为增函数,且函数y=f(x+6)为偶函数,则( )| A. | f(4)<f(7) | B. | f(4)>f(7) | C. | f(5)>f(7) | D. | f(5)<f(7) |
分析 根据题意,由y=f(x+6)为偶函数,可得函数y=f(x)的图象关于直线x=6对称,分析可得f(4)=f(8),f(5)=f(7);可以判定C、D错误,再结合函数在(6,+∞)上的单调性,可得f(8)>f(7),又由f(4)=f(8),即可得f(4)>f(7);综合可得答案.
解答 解:根据题意,y=f(x+6)为偶函数,则函数f(x)的图象关于x=6对称,
f(4)=f(8),f(5)=f(7);
故C、D错误;
又由函数在(6,+∞)上为增函数,则有f(8)>f(7);
又由f(4)=f(8),
故有f(4)>f(7);
故选:B.
点评 本题考查函数的单调性与奇偶性,其中根据已知分析出函数y=f(x)的图象关于直线x=6对称是解题的关键.

练习册系列答案
相关题目
4.若函数$f(x)=\frac{d}{{a{x^2}-bx+c}}(a,b,c,d∈R)$的图象如图所示,则a:b:c:d=( )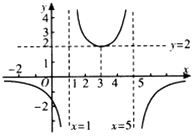

| A. | 1:6:5:(-8) | B. | 1:6:5:8 | C. | 1:(-6):5:8 | D. | 1:(-6):5:(-8) |
1.某厂生产总值连续两年持续增加,第一年的增长率为a,第二年的增长率为b,则该厂这两年生产总值的年平均增长率为( )
| A. | $\frac{a+b}{2}$ | B. | $\sqrt{ab}$ | C. | $\sqrt{(a+1)(b+1)}-1$ | D. | $\sqrt{(a+1)(b+1)}+1$ |
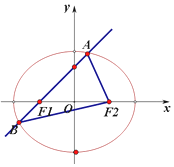 如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).
如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).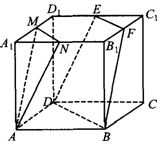 如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.
如图,已知棱长为4的正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1D1,A1B1,D1C1,B1C1的中点,求证:平面AMN∥平面EFBD.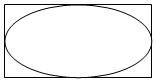 如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为60颗,以此实验数据为依据可以估算椭圆的面积约为( )