题目内容
6．在△ABC中，已知a，b，c三边上的高ha=3，hb=4，hc=5，则sinA：sinB：sinC=20：15：12．分析 由题意和三角形的面积公式列出方程，化简后得到a、b、c的关系，求出a：b：c的值，由正弦定理即可求出sinA：sinB：sinC的值．
解答 解：∵a，b，c三边上的高ha=3，hb=4，hc=5，
∴$\frac{1}{2}×a×3=\frac{1}{2}×b×4=\frac{1}{2}×c×5$，
则3a=4b=5c，即b=$\frac{3}{4}$a，c=$\frac{3}{5}$a，
∴a：b：c=20：15：12，
由正弦定理得，
sinA：sinB：sinC=a：b：c=20：15：12，
故答案为：20：15：12．
点评 本题考查正弦定理，以及三角形的面积公式的应用，考查化简、变形能力．
练习册系列答案
相关题目
16．定义在R上的函数f（x）在（6，+∞）上为增函数，且函数y=f（x+6）为偶函数，则（ ）
| A． | f（4）＜f（7） | B． | f（4）＞f（7） | C． | f（5）＞f（7） | D． | f（5）＜f（7） |
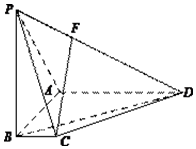如图，在四棱锥P-ABCD中，PB⊥底面ABCD，底面ABCD为梯形，AD∥BC，AD⊥AB，且PB=AB=AD=3，BC=1．
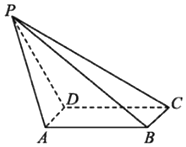如图，在四棱锥P-ABCD中，底面ABCD是矩形，AD⊥PD，BC=1，PC=2$\sqrt{3}$，PD=CD=2，则二面角A-PB-C的正切值为$\frac{\sqrt{15}}{9}$．
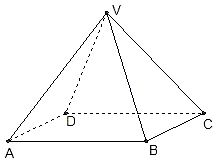如图，四棱锥V-ABCD中，底面ABCD是边长为2的正方形，其它侧面都是侧棱长为$\sqrt{5}$的等腰三角形，试画出二面角V-AB-C的平面角，并求出它的度数．
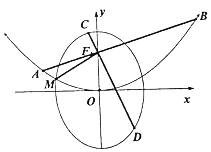已知F1为椭圆C1：$\frac{{y}^{2}}{{a}^{2}}+\frac{{x}^{2}}{{b}^{2}}$=1的上焦点，F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=$\frac{5}{3}$．