题目内容
16.设命题p:?x0∈R,x${\;}_{0}^{2}$-1>0,则¬p为( )| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |
分析 根据特称命题的否定是全称命题进行判断即可.
解答 解:命题是特称命题,则命题的否定是:
?x∈R,x2-1≤0,
故选:C
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
相关题目
7.设F是椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{4}$=1的左焦点,P为椭圆上一点,M是PF的中点,且|PF|=4,则坐标原点O到点M的距离是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.直线3x-y=0绕原点逆时针旋转90°,再向右平移1个单位,所得到直线的方程为( )
| A. | x+3y-3=0 | B. | x+3y-1=0 | C. | 3x-y-3=0 | D. | x-3y+3=0 |
6.若纯虚数z满足(1-i)z=1+ai,则实数a等于( )
| A. | 0 | B. | -1或1 | C. | -1 | D. | 1 |
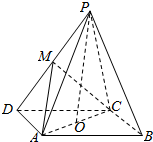 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.