题目内容
4.已知方程$\left\{\begin{array}{l}{x=1+tsinα}\\{y=1+tcosα}\end{array}\right.$.(1)当常数α∈(0,π),t为参数时,求该直线的倾斜角;
(2)当t=2,α为参数时,过点P(0,1)作直线l与己知方程的曲线相交于两个不同的点A,B,求|PA|+|PB|的取值范围.
分析 (1)k=$\frac{cosα}{sinα}$=$\frac{sin(\frac{π}{2}-α)}{cos(\frac{π}{2}-α)}$=$tan(\frac{π}{2}-α)$,即可得出该直线的倾斜角.
(2)当t=2,α为参数时,化为(x-1)2+(y-1)2=4,设过点P(0,1)的直线l方程为:$\left\{\begin{array}{l}{x=mcosθ}\\{y=1+msinθ}\end{array}\right.$,m为参数,θ∈[0,2π).代入圆的方程可得:m2-2mcosθ-3=0.利用根与系数的关系可得:|PA|+|PB|=|m1-m2|=$\sqrt{({m}_{1}+{m}_{2})^{2}-4{m}_{1}{m}_{2}}$.
解答 解:(1)k=$\frac{cosα}{sinα}$=$\frac{sin(\frac{π}{2}-α)}{cos(\frac{π}{2}-α)}$=$tan(\frac{π}{2}-α)$,∵常数α∈(0,π),∴该直线的倾斜角为$\frac{π}{2}$-α.
(2)当t=2,α为参数时,化为(x-1)2+(y-1)2=4,
设过点P(0,1)的直线l方程为:$\left\{\begin{array}{l}{x=mcosθ}\\{y=1+msinθ}\end{array}\right.$,m为参数,θ∈[0,2π).
代入圆的方程可得:m2-2mcosθ-3=0.
∴m1+m2=2cosθ,m1m2=-3.
∴|PA|+|PB|=|m1-m2|=$\sqrt{({m}_{1}+{m}_{2})^{2}-4{m}_{1}{m}_{2}}$=$\sqrt{4co{s}^{2}θ+12}$=$2\sqrt{co{s}^{2}θ+3}$∈$[2\sqrt{3},4]$.
∴|PA|+|PB|的取值范围是$[2\sqrt{3},4]$.
点评 本题考查了圆的参数方程化为普通方程、同角三角函数基本关系式、直线参数方程的应用、直线的倾斜角,考查了推理能力与计算能力,属于中档题.

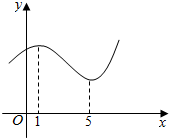
| A. | f′(3)>3 | B. | f′(3)<3 | C. | f′(3)=3 | D. | f′(3)的符号不确定 |
| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |

| A. | 4 | B. | 5 | C. | 6 | D. | 8 |

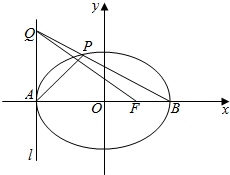 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.