题目内容
8.椭圆W的中心在坐标原点O,以坐标轴为对称轴,且过点$(0,\sqrt{3})$,其右焦点为F(1,0).过原点O作直线l1交椭圆W于A,B两点,过F作直线l2交椭圆W于C,D两点,且$\overrightarrow{AB}$∥$\overrightarrow{CD}$.(Ⅰ)求椭圆W的标准方程;
(Ⅱ)求证:|AB|2=4|CD|.
分析 (Ⅰ)设椭圆W的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,a>b>0.利用真假求解即可.
(Ⅱ)当直线l1垂直于x轴时,推出|AB|2=4|CD|.
当直线l1不垂直于x轴时,设直线l1的斜率为k,则依题意l2的斜率也为k,其方程为y=k(x-1).设点A(x0,y0),B(-x0,-y0),C(x1,y1),D(x2,y2).求出${|{AB}|^2}=4({x_0^2+y_0^2})$.把y=k(x-1)代入椭圆方程中,整理得,通过判别式,韦达定理以及弦长公式,证明|AB|2=4|CD|.
解答 (本题满分14分)
解:(Ⅰ)因为已知焦点在x轴上,设椭圆W的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,a>b>0.
由题意:$b=\sqrt{3},c=1$,则a2=4.
所求椭圆W的标准方程为:$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(4分)
(Ⅱ)当直线l1垂直于x轴时,则直线l2也垂直于x轴,把x=1代入椭圆W的方程,得$y=±\frac{3}{2}$,即此时|CD|=3,而$|{AB}|=2\sqrt{3}$,所以|AB|2=4|CD|.
当直线l1不垂直于x轴时,设直线l1的斜率为k,则依题意l2的斜率也为k,其方程为y=k(x-1).设点A(x0,y0),B(-x0,-y0),C(x1,y1),D(x2,y2).
则${|{AB}|^2}=4({x_0^2+y_0^2})$.
把y=k(x-1)代入椭圆方程中,整理得,(4k2+3)x2-8k2x+4k2-12=0.
显然△>0,${x_1}+{x_2}=\frac{{8{k^2}}}{{4{k^2}+3}}$,${x_1}{x_2}=\frac{{4{k^2}-12}}{{4{k^2}+3}}$.
则$|{CD}|=\sqrt{({x_1}-{x_2}{)^2}+({y_1}-{y_2}{)^2}}=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$=$\sqrt{1+{k^2}}$$\sqrt{({x_1}+{x_2}{)^2}-4{x_1}{x_2}}$.
即|CD|=$\sqrt{1+{k^2}}$$\sqrt{\frac{{144({k^2}+1)}}{{{{(4{k^2}+3)}^2}}}}$=$\frac{{12({k^2}+1)}}{{4{k^2}+3}}$.
由${|{AB}|^2}=4({x_0^2+y_0^2})$,且A(x0,y0)在椭圆上,
得${|{AB}|^2}=4[{{x_0}^2+3(1-\frac{{{x_0}^2}}{4})}]=4(\frac{{{x_0}^2}}{4}+3)$.
则|AB|2(4k2+3)=$4{k^2}x_0^2+3x_0^2+48{k^2}+36$.
因为直线l1过原点,所以y0=kx0,则|AB|2(4k2+3)=$4y_0^2+3x_0^2+48{k^2}+36$.
因为A(x0,y0)在椭圆上,所以$3x_0^2+4y_0^2=12$,所以|AB|2(4k2+3)=48(k2+1).
所以|AB|2(4k2+3)=4×12(k2+1),即|AB|2=4|CD|.…(14分)
点评 本题考查椭圆的标准方程的求法,直线与椭圆的位置关系的综合应用,考查分类讨论以及转化思想的应用,考查计算能力.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |
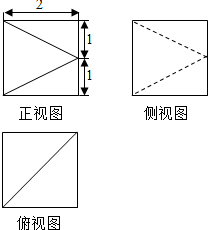
| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{22}{3}$ |

| A. |  | B. |  | C. |  | D. |  |
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).