题目内容
6.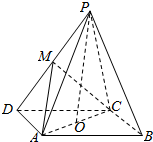 如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.
如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,∠ADC=45°,AD=AC=1,PO⊥平面ABCD,O点在AC上,PO=2,M为PD中点.(1)证明:AD⊥平面PAC;
(2)求三棱锥M-ACD的体积.
分析 (1)由PO⊥平面ABCD可得PO⊥AD,由∠ADC=45°,AD=AC可知△ACD是直角三角形,AC⊥AD.故AD⊥平面PAC;
(2)由M为中点可知M到底面的距离为$\frac{1}{2}$PO,把△ACD看做棱锥的底面,则棱锥的高为$\frac{1}{2}PO$,代入体积公式计算.
解答 证明:(1)∵AD=AC,∴∠ACD=∠ADC=45°,∴AD⊥AC.
∵PO⊥平面ABCD,AD?平面ABCD,
∴PO⊥AD,又∵AC?平面PAC,PO?平面PAC,
∴AD⊥平面PAC.
(2)∵M是PD的中点,∴M到平面ABCD的距离d=$\frac{1}{2}$PO=1.
S△ACD=$\frac{1}{2}AD×AC$=$\frac{1}{2}$.
∴三棱锥M-ACD的体积V=$\frac{1}{3}$S△ACD•d=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
点评 本题考查了线面垂直的判定,棱锥的体积计算,属于基础题.

练习册系列答案
相关题目
14.函数y=f(x)的图象如图,则( )
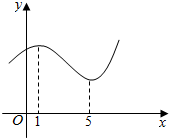

| A. | f′(3)>3 | B. | f′(3)<3 | C. | f′(3)=3 | D. | f′(3)的符号不确定 |
1.如图1,已知正方体ABCD-A1B1C1D1的棱长为a,动点M、N、Q分别在线段AD1、B1C、C1D1上,当三棱锥Q-BMN的正视图如图所示时,三棱锥Q-BMN的侧视图的面积等于( )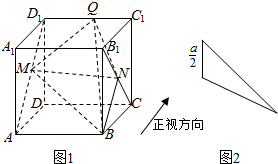

| A. | $\frac{1}{4}{a}^{2}$ | B. | $\frac{3}{4}{a}^{2}$ | C. | $\frac{1}{2}{a}^{2}$ | D. | $\frac{\sqrt{3}}{2}{a}^{2}$ |
16.设命题p:?x0∈R,x${\;}_{0}^{2}$-1>0,则¬p为( )
| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |
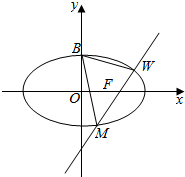 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{2}}{2}$,上顶点为B(0,1).