题目内容
1.已知抛物线C:y2=-4x的焦点F,A(-1,1),则曲线C上的动点P到点F与点A的距离之和的最小值为2.分析 根据抛物线方程求出焦点坐标和准线方程,再由抛物线的定义知:当P、A和P在准线上的射影点Q三点共线时,这个距离之和最小,即可得出结论.
解答 解:∵抛物线方程为y2=-4x,
∴2p=4,可得焦点为F(-1,0),准线为x=1
设P在抛物线准线l上的射影点为Q点,A(-1,1)
则由抛物线的定义,可知当P、Q、A点三点共线时,点P到点(-1,1)的距离与P到该抛物线焦点的距离之和最小,
∴最小值为1+1=2.
故答案为:2.
点评 本题给出抛物线上的动点,求该点到定点Q和焦点F距离之和的最小值,着重考查了抛物线的定义和简单几何性质等知识,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.设命题p:?x0∈R,x${\;}_{0}^{2}$-1>0,则¬p为( )
| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |
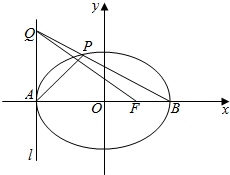 如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.
如图,A、B分别是椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1(2>b>0)的左右顶点,F为其右焦点,|AF|×|FB|=3.