题目内容
11.设数列{an}的前n项和为Sn,其中an≠0,a1=1,且a1,Sn,an+1(n∈N*)成等差数列,则a2016=32014.分析 通过a1,Sn,an+1(n∈N*)成等差数列及a1=1可知2Sn=a1+an+1=1+an+1,并与当n≥2时2Sn-1=1+an作差,整理可知数列{an}从第二项起是首项为1、公比为3的等比数列,进而计算即得结论.
解答 解:∵a1,Sn,an+1(n∈N*)成等差数列,且a1=1,
∴2Sn=a1+an+1=1+an+1,
当n≥2时,2Sn-1=1+an,
两式相减得:2an=an+1-an,
即an+1=3an(n≥2),
又∵a2=2S1-1=1,
∴数列{an}从第二项起是首项为1、公比为3的等比数列,
∴a2016=32014,
故答案为:32014.
点评 本题考查数列的通项,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
1.如图1,已知正方体ABCD-A1B1C1D1的棱长为a,动点M、N、Q分别在线段AD1、B1C、C1D1上,当三棱锥Q-BMN的正视图如图所示时,三棱锥Q-BMN的侧视图的面积等于( )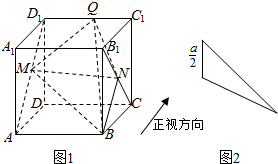

| A. | $\frac{1}{4}{a}^{2}$ | B. | $\frac{3}{4}{a}^{2}$ | C. | $\frac{1}{2}{a}^{2}$ | D. | $\frac{\sqrt{3}}{2}{a}^{2}$ |
16.设命题p:?x0∈R,x${\;}_{0}^{2}$-1>0,则¬p为( )
| A. | ?x0∈R,x${\;}_{0}^{2}$-1≤0 | B. | ?x0∈R,x${\;}_{0}^{2}$-1<0 | ||
| C. | ?x∈R,x2-1≤0 | D. | ?x∈R,x2-1<0 |
3.某几何体的三视图如图所示,则该几何体的体积为( )
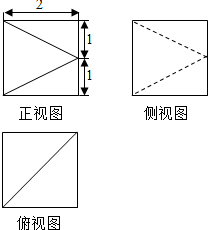

| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{20}{3}$ | D. | $\frac{22}{3}$ |