题目内容

已知函数f（x）=sin（3x+
π
4
）．若α是第二象限的角，f（
α
3
）=
4
5
cos（α+
π
4
）cos2α，求cosα-sinα的值．
考点：二倍角的余弦
专题：三角函数的求值
分析：依题意知f（
α
3
）=sin（α+
π
4
）=
4
5
cos（α+
π
4
）×2cos（α+
π
4
）sin（α+
π
4
），整理可得cos2(α+
π
4
)=
5
8
；①，进一步分析可知cosα-sinα=
2
cos（α+
π
4
）＜0，②二者联立即可求得cosα-sinα的值．
解答： 解：∵f（x）=sin（3x+
π
4
），
∴f（
α
3
）=sin（α+
π
4
），又f（
α
3
）=
4
5
cos（α+
π
4
）cos2α=
4
5
cos（α+
π
4
）sin（2α+
π
2
），
∴
4
5
cos（α+
π
4
）×2cos（α+
π
4
）sin（α+
π
4
）=sin（α+
π
4
），
依题意知sin（α+
π
4
）≠0，
∴cos2(α+
π
4
)=
5
8
；①
∵α是第二象限的角，
∴cosα＜0，sinα＞0，
∴cosα-sinα=
2
cos（α+
π
4
）＜0，②
由①②得：cos（α+
π
4
）=-
10
4
，
∴cosα-sinα=
2
×（-
10
4
）=-
5
2
．
点评：本题考查二倍角的正弦，求得cos2(α+
π
4
)=
5
8
与cosα-sinα=
2
cos（α+
π
4
）＜0是关键，也是难点，考查等价转化思想与运算求解能力，属于中档题．
练习册系列答案
相关题目
阅读下列算法程序框图，若输出的结果S为
3
，则判断框中的横线上最小正整数值为（　　）
A、1B、2C、3D、4
已知函数f（x）=4sinx•sin2（
π
4
+
x
2
）+2cos2x+1+a，x∈R是一个奇函数．
（1）求a的值和使f（2x）≥-
3
成立的x的取值集合；
（2）设|θ|＜
π
2
，若对x取一切实数，不等式4+f（x+θ）f（x-θ）＞2f（x）都成立，求θ的取值范围．
已知tanα=3，求2sin2α+5cos2α的值．
已知变量x，y满足约束条件
y≥2x-2
y≥-x-1
y≤
1
2
x+1
，则z=y-x的最小值为
 
．
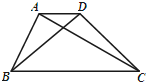如图，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．
（Ⅰ）求sin∠ABC；
（Ⅱ）求BD的长度．
设函数f（x）=ex+sinx，g（x）=ax，且F（x）=f（x）-g（x）．
（1）若F（x）≥1在[0，+∞）上恒成立，求实数a的取值范围；
（2）当a=
1
3
时，存在x1、x2∈[0，+∞），使f（x1）=g（x2）成立，求x2-x1的最小值．
用指定方法法证明不等式：
3
+
5
＞
2
+
6
．
（Ⅰ）分析法；
（Ⅱ）反证法．
已知直线l过点A（-1，1），且在y上的截矩是在x轴上的截距的2倍，求直线l的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网