题目内容
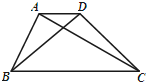如图，在梯形ABCD中，AD∥BC，AB=5，AC=9，∠BCA=30°，∠ADB=45°．（Ⅰ）求sin∠ABC；
（Ⅱ）求BD的长度．
考点：正弦定理的应用,解三角形的实际应用
专题：解三角形
分析：（Ⅰ）由正弦定理求得sin∠ABC的值．
（Ⅱ）先求得∠BAD，进而求得sin∠ABC，最后利用正弦定理求得BD．
（Ⅱ）先求得∠BAD，进而求得sin∠ABC，最后利用正弦定理求得BD．
解答：
解：（Ⅰ）在△ABC中，由正弦定理，得
=
，
∴sin∠ABC=
=
=
．
（Ⅱ）∵AD∥BC，
∴∠BAD=180°-∠ABC，
sin∠BAD=sin(180°-∠ABC)=sin∠ABC=
，
在△ABD中，由正弦定理，得
=
，
∴BD=
=
=
．
| AB |
| sin∠BCA |
| AC |
| sin∠ABC |
∴sin∠ABC=
| ACsin∠BCA |
| AB |
| 9sin30° |
| 5 |
| 9 |
| 10 |
（Ⅱ）∵AD∥BC，
∴∠BAD=180°-∠ABC，
sin∠BAD=sin(180°-∠ABC)=sin∠ABC=
| 9 |
| 10 |
在△ABD中，由正弦定理，得
| AB |
| sin∠ADB |
| BD |
| sin∠BAD |
∴BD=
| ABsin∠BAD |
| sin∠ADB |
5×
| ||||
|
9
| ||
| 2 |
点评：本题主要考查了正弦定理的应用．作为解三角形问题的常用公式，应熟练记忆．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
矩阵
的逆矩阵是（ ）
|
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
一个几何体的三视图如图所示，其中主视图是边长为3cm的正方形，俯视图是半圆，求该几何体的表面积．