题目内容
13．《九章算术》是我国古代的数学巨著，内容极为丰富，书中有如下问题：“今有五人分五钱，令上二人所得与下三人等，问各得几何．”意思是：“5人分取5钱，各人所得钱数依次成等差数列，其中前2人所得钱数之和与后3人所得钱数之和相等．”，则其中分得钱数最多的是（ ）| A． | $\frac{5}{6}$钱 | B． | 1钱 | C． | $\frac{7}{6}$钱 | D． | $\frac{4}{3}$钱 |
分析 依题意设5人所得钱分别为a-2d，a-d，a，a+d，a+2d，由题意求得a=-6d，结合a-2d+a-d+a+a+d+a+2d=5a=5求得a=1，则答案可求．
解答 解：依题意设5人所得钱分别为a-2d，a-d，a，a+d，a+2d，
则由题意可知，a-2d+a-d=a+a+d+a+2d，即a=-6d，
又a-2d+a-d+a+a+d+a+2d=5a=5，∴a=1，
则a-2d=a-2×（-$\frac{a}{6}$）=$\frac{4}{3}$a=$\frac{4}{3}$．
故选：D
点评 本题考查等差数列的通项公式，是基础的计算题．
练习册系列答案
相关题目
4．若函数f（x）=ex（sinx+acosx）在（$\frac{π}{4}$，$\frac{π}{2}$）上单调递增，则实数a的取值范围是（ ）
| A． | （-∞，1] | B． | （-∞，1） | C． | [1，+∞） | D． | （1，+∞） |
1．已知Sn是等差数列{an}的前n项和，则2（a1+a3+a5）+3（a8+a10）=36，则S11=（ ）
| A． | 66 | B． | 55 | C． | 44 | D． | 33 |
8．数列{an}中，已知a1=1，a2=2，an+2=an+1-an（n∈N*），则a2017=（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | 2 |
18．为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况，从两校各随机抽取60名学生，将所得样本作出频数分布统计表如下：
甲校：
乙校：
以抽样所得样本数据估计总体
（1）比较甲、乙两校学生的数学平均成绩的高低；
（2）若规定数学成绩不低于120分为优秀，从甲、乙两校全体高三学生中各随机抽取2人，其中数学成绩为优秀的共X人，求X的分布列及数学期望．
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 15 | 6 | 6 | 3 |
（1）比较甲、乙两校学生的数学平均成绩的高低；
（2）若规定数学成绩不低于120分为优秀，从甲、乙两校全体高三学生中各随机抽取2人，其中数学成绩为优秀的共X人，求X的分布列及数学期望．
5．
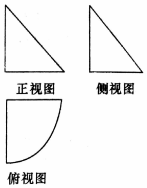一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的等腰直角三角形，俯视图是圆心角为$\frac{π}{2}$的扇形，则该几何体的表面积为（ ）
一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的等腰直角三角形，俯视图是圆心角为$\frac{π}{2}$的扇形，则该几何体的表面积为（ ）| A． | 2 | B． | π+4 | C． | $\sqrt{2}π+4$ | D． | $（{\sqrt{2}+1}）π+4$ |
2．在区间[0，1]上随机取两个数，则这两个数之和小于$\frac{3}{2}$的概率是（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{7}{8}$ |