题目内容
18.为了了解甲、乙两所学校全体高三年级学生在该地区八校联考中的数学成绩情况,从两校各随机抽取60名学生,将所得样本作出频数分布统计表如下:甲校:
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 5 | 9 | 10 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 14 | 10 | 6 | 4 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 2 | 4 | 8 | 16 |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] |
| 频数 | 15 | 6 | 6 | 3 |
(1)比较甲、乙两校学生的数学平均成绩的高低;
(2)若规定数学成绩不低于120分为优秀,从甲、乙两校全体高三学生中各随机抽取2人,其中数学成绩为优秀的共X人,求X的分布列及数学期望.
分析 (1)计算甲、乙的平均数,比较即可得出结论;
(2)由题意知,甲、乙两校学生的优秀率分别为$\frac{1}{4}$、$\frac{1}{3}$,X的可能取值是0,1,2,3,4;计算对应的概率,写出X的分布列,求出数学期望值.
解答 解:(1)计算甲的平均数为
$\overline{{x}_{甲}}$=$\frac{1}{60}$×(75×2+85×4+95×8+105×16+115×15+125×6+135×6+145×3)=110.8,…(2分)
乙的平均数为
$\overline{{x}_{乙}}$=$\frac{1}{60}$×(75×2+85×5+95×9+105×10+115×14+125×10+135×6+145×4)=112.2;…(4分)
所以乙校学生的数学平均成绩高于甲校;…(5分)
(2)由上表可知,甲、乙两校学生的优秀率分别为$\frac{1}{4}$、$\frac{1}{3}$,
X=0,1,2,3,4;…(6分)
P(X=0)=${(\frac{3}{4})}^{2}$×${(\frac{2}{3})}^{2}$=$\frac{36}{144}$,P(X=1)=${C}_{2}^{1}$•$\frac{3}{4}$•$\frac{1}{4}$•${(\frac{2}{3})}^{2}$+${C}_{2}^{1}$•${(\frac{3}{4})}^{2}$•$\frac{1}{3}$•$\frac{2}{3}$=$\frac{60}{144}$,
P(X=2)=${(\frac{3}{4})}^{2}$×${(\frac{1}{3})}^{2}$+${(\frac{1}{4})}^{2}$×${(\frac{2}{3})}^{2}$+${C}_{2}^{1}$•$\frac{3}{4}$•$\frac{1}{4}$•${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$=$\frac{37}{144}$,
P(X=3)=${(\frac{1}{4})}^{2}$•${C}_{2}^{1}$•$\frac{2}{3}$•$\frac{1}{3}$+${C}_{2}^{1}$•$\frac{3}{4}$•$\frac{1}{4}$•${(\frac{1}{3})}^{2}$=$\frac{10}{144}$,
P(X=4)=${(\frac{1}{4})}^{2}$×${(\frac{1}{3})}^{2}$=$\frac{1}{144}$;
所以X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{36}{144}$ | $\frac{60}{144}$ | $\frac{37}{144}$ | $\frac{10}{144}$ | $\frac{1}{144}$ |
数学期望为E(X)=0×$\frac{36}{144}$+1×$\frac{60}{144}$+2×$\frac{37}{144}$+3×$\frac{10}{144}$+4×$\frac{1}{144}$=$\frac{7}{6}$.…(12分)
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,是基础题.

| A. | e | B. | 2e | C. | 1 | D. | 2 |
| A. | $\frac{5}{6}$钱 | B. | 1钱 | C. | $\frac{7}{6}$钱 | D. | $\frac{4}{3}$钱 |
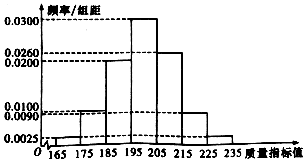 某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:| 质量指标值m | m<185 | 185≤m<205 | M≥205 |
| 等级 | 三等品 | 二等品 | 一等品 |
(1)根据以上抽样调查的数据,能否认为该企业生产这种产品符合“一、二等品至少要占到全部产品的92%的规定”?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品的质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(218,140),则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?