题目内容
4.若函数f(x)=ex(sinx+acosx)在($\frac{π}{4}$,$\frac{π}{2}$)上单调递增,则实数a的取值范围是( )| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
分析 f(x)=ex(sinx+acosx)在($\frac{π}{4}$,$\frac{π}{2}$)上单调递增,求导,分离参数,构造函数,利用导数求出函数的最值即可.
解答 解:∵f(x)=ex(sinx+acosx)在($\frac{π}{4}$,$\frac{π}{2}$)上单调递增,
∴f′(x)=ex[(1-a)sinx+(1+a)cosx]≥0在($\frac{π}{4}$,$\frac{π}{2}$)上恒成立,
∵ex>0在($\frac{π}{4}$,$\frac{π}{2}$)上恒成立,
∴(1-a)sinx+(1+a)cosx≥0在($\frac{π}{4}$,$\frac{π}{2}$)上恒成立,
∴a(sinx-cosx)≤sinx+cosx在($\frac{π}{4}$,$\frac{π}{2}$)上恒成立
∴a≤$\frac{sinx+cosx}{sinx-cosx}$,
设g(x)=$\frac{sinx+cosx}{sinx-cosx}$,
∴g′(x)=$\frac{-2}{(sinx-cosx)^{2}}$<0在($\frac{π}{4}$,$\frac{π}{2}$)上恒成立,
∴g(x)在($\frac{π}{4}$,$\frac{π}{2}$)上单调递减,
∴g(x)>g($\frac{π}{2}$)=1,
∴a≤1,
故选:A.
点评 本题考查了导数和函数的单调性和最值得关系,关键是分离参数,构造函数,属于中档题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
18.在等差数列{an}中,若a4-a2=-2,a7=-3,则a9=( )
| A. | 2 | B. | -2 | C. | -5 | D. | -4 |
15.已知全集U=R,集合A={x|x<2},B={x|x<0},那么A∩∁UB=( )
| A. | {x|0≤x<2} | B. | {x|0<x<2} | C. | {x|x<0} | D. | {x|x<2} |
13.《九章算术》是我国古代的数学巨著,内容极为丰富,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”,则其中分得钱数最多的是( )
| A. | $\frac{5}{6}$钱 | B. | 1钱 | C. | $\frac{7}{6}$钱 | D. | $\frac{4}{3}$钱 |
14.已知圆M与直线3x-4y=0及3x-4y+10=0都相切,圆心在直线y=-x-4上,则圆M的方程为( )
| A. | (x+3)2+(y-1)2=1 | B. | (x-3)2+(y+1)2=1 | C. | (x+3)2+(y+1)2=1 | D. | (x-3)2+(y-1)2=1 |
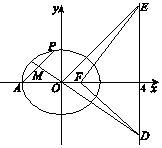 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.