题目内容
8.数列{an}中,已知a1=1,a2=2,an+2=an+1-an(n∈N*),则a2017=( )| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
分析 利用已知可得an+6=an.可得a2017=a6×334+3=a3.
解答 解:∵a1=1,a2=2,an+2=an+1-an(n∈N*),∴a3=2-1=1,
同理可得:a4=-1,a5=-2,a6=-1,a7=1,a8=2.….
∴an+6=an.
则a2017=a6×334+3=a3=1.
故选:A.
点评 本题考查了数列递推关系、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.若函数y=f(x)的图象上每一点的纵坐标保持不变,横坐标伸长到原来的2倍,再将整个图象沿x轴向右平移$\frac{π}{2}$个单位,沿y轴向下平移1个单位,得到函数y=$\frac{1}{2}$sinx的图象,则y=f(x)的解析式为( )
| A. | y=$\frac{1}{2}$sin(2x+$\frac{π}{2}$)+1 | B. | y=$\frac{1}{2}$sin(2x-$\frac{π}{2}$)+1 | C. | y=$\frac{1}{2}$sin($\frac{1}{2}$x+$\frac{π}{4}$)+1 | D. | y=$\frac{1}{2}$sin($\frac{1}{2}$x-$\frac{π}{4}$)+1 |
13.《九章算术》是我国古代的数学巨著,内容极为丰富,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”,则其中分得钱数最多的是( )
| A. | $\frac{5}{6}$钱 | B. | 1钱 | C. | $\frac{7}{6}$钱 | D. | $\frac{4}{3}$钱 |
20.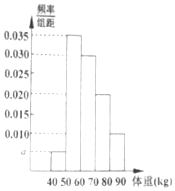 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
 从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )
从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成频率分布直方图(如图),由直方图可知( )| A. | 估计体重的众数为50或60 | |
| B. | a=0.03 | |
| C. | 学生体重在[50,60)有35人 | |
| D. | 从这100名男生中随机抽取一人,体重在[60,80)的概率为$\frac{1}{3}$ |
17.已知函数h(x)的图象与函数g(x)=ex的图象关于直线y=x对称,点A在函数f(x)=ax-x2($\frac{1}{e}≤x≤e$,e为自然对数的底数)上,A关于x轴对称的点A'在函数h(x)的图象上,则实数a的取值范围是( )
| A. | $[{1,e+\frac{1}{e}}]$ | B. | $[{1,e-\frac{1}{e}}]$ | C. | $[{e-\frac{1}{e},e+\frac{1}{e}}]$ | D. | $[{e-\frac{1}{e},e}]$ |
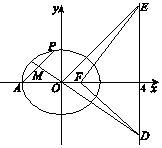 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{1}{2}$,F为椭圆C的右焦点.A(-a,0),|AF|=3.