题目内容
过点(-1,1)的直线与圆x2+y2-2x-4y-11=0截得的弦长为4
,则该直线的方程为 .
| 3 |
考点:直线与圆相交的性质
专题:直线与圆
分析:分类讨论:过点(-1,1)的直线与x轴垂直时,直接验证即可;过点(-1,1)的直线与x轴垂直时,设直线的方程为:y-1=k(x+1),利用点到直线的距离公式可得:圆心C到此直线的距离d.利用弦长公式4
=2
,即可解得k.
| 3 |
| r2-d2 |
解答:
解:由圆x2+y2-2x-4y-11=0化为:(x-1)2+(y-2)2=16,得到圆心C(1,2),半径r=4.
①过点(-1,1)的直线与x轴垂直时,把x=-1代入圆的方程:(-1)2+y2-2×(-1)-4y-11=0,
化为y2-4y-8=0,解得y1=2-2
,y2=2+2
.
∴弦长=y2-y1=4
.满足题意.
②过点(-1,1)的直线与x轴垂直时,设直线的方程为:y-1=k(x+1),即kx-y+k+1=0.
圆心C到此直线的距离d=
=
.
∴4
=2
,即2
=
,化为4k=-3,解得k=-
.
∴直线的方程为:-
x-y-
+1=0,化为3x+4y-1=0.
综上可知:所求直线的方程为x=-1或3x+4y-1=0.
故答案为:x=-1或3x+4y-1=0.
①过点(-1,1)的直线与x轴垂直时,把x=-1代入圆的方程:(-1)2+y2-2×(-1)-4y-11=0,
化为y2-4y-8=0,解得y1=2-2
| 3 |
| 3 |
∴弦长=y2-y1=4
| 3 |
②过点(-1,1)的直线与x轴垂直时,设直线的方程为:y-1=k(x+1),即kx-y+k+1=0.
圆心C到此直线的距离d=
| |k-2+k+1| | ||
|
| |2k-1| | ||
|
∴4
| 3 |
| r2-d2 |
| 3 |
16-(
|
| 3 |
| 4 |
∴直线的方程为:-
| 3 |
| 4 |
| 3 |
| 4 |
综上可知:所求直线的方程为x=-1或3x+4y-1=0.
故答案为:x=-1或3x+4y-1=0.
点评:本题考查了直线与圆相交的问题、弦长公式、点到直线的距离公式、分类讨论等基础知识与基本技能方法,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在△ABC中,a、b、c分别是角A、B、C的对边,若a2+b2=2014c2,则
的值为( )
| 2tanA•tanB |
| tanC(tanA+tanB) |
| A、0 | B、1 |
| C、2013 | D、2014 |
两条不重合的直线l1和l2的方向向量分别为
=(1,-1,2),
=(0,2,1),则l1与l2的位置关系是( )
| v1 |
| v2 |
| A、平行 | B、相交 | C、垂直 | D、不确定 |
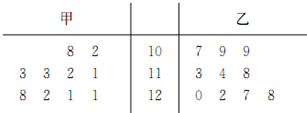 为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)
为调查某次考试数学的成绩,随机抽取某中学甲、乙两班各十名同学,获得成绩数据的茎叶图如图(单位:分)