题目内容
△ABC的三个内角A,B,C所对的边分别为a,b,c且asinAsinB+bcos2A=
a,则
= .
| 2 |
| b |
| a |
考点:正弦定理,解三角形
专题:计算题,解三角形
分析:由正弦定理与同角三角函数的平方关系,化简整理题中的等式得sinB=
sinA,从而得到b=
a,可得答案.
| 2 |
| 2 |
解答:
解:∵△ABC中,asinAsinB+bcos2A=
a,
∴根据正弦定理,得sin2AsinB+sinBcos2A=
sinA,
可得sinB(sin2A+cos2A)=
sinA,
∵sin2A+cos2A=1,
∴sinB=
sinA,得b=
a,可得
=
.
故答案为:
| 2 |
∴根据正弦定理,得sin2AsinB+sinBcos2A=
| 2 |
可得sinB(sin2A+cos2A)=
| 2 |
∵sin2A+cos2A=1,
∴sinB=
| 2 |
| 2 |
| b |
| a |
| 2 |
故答案为:
| 2 |
点评:本题给出三角形满足的边角关系式,求边a、b的比值.着重考查了正弦定理、同角三角函数的基本关系等知识,属于基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
已知偶函数f(x)在区间[0,+∞)单调递减,则满足f(lnx)>f(1)的x取值范围是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
| D、(0,1)∪(e,+∞) |
已知条件p:x2-3x-4≤0,条件q:x2-6x+9-m2≤0(m>0).若p是q的充分不必要条件,则正数m的取值范围为( )
| A、(0,1] |
| B、(0,4] |
| C、[1,+∞) |
| D、[4,+∞) |
在可行域内任取一点,其规则如流程图所示,则能输出数对(x,y)的概率是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
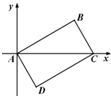 如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,
如图,在平面直角坐标系中,已知平行四边形ABCD的三个顶点坐标:A(0,0),B(3,