题目内容
7.定义在R上的函数y=f(x),当x∈[0,2]时,f(x)=4(1-|x-1|),且对任意实数x∈[2n-2,2n+1-2](n∈N*,n≥2),都有f(x)=$\frac{1}{2}$f($\frac{x}{2}$-1).若g(x)=f(x)-logax有且仅有3个零点,则实数a的取值范围是( )| A. | [2,10] | B. | [$\sqrt{2}$,$\sqrt{10}$] | C. | (2,10) | D. | [2,10) |
分析 由g(x)=f(x)-logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,利用数形结合即可得到结论.
解答 解:当x∈[0,2]时,f(x)=4(1-|x-1|),
当n=2时,x∈[2,6],此时$\frac{x}{2}$-1∈[0,2],则f(x)=$\frac{1}{2}$f($\frac{x}{2}$-1)=$\frac{1}{2}$×4(1-|$\frac{x}{2}$-1-1|)=2(1-|$\frac{x}{2}$-2|),
当n=3时,x∈[6,14],此时$\frac{x}{2}$-1∈[2,6],则f(x)=$\frac{1}{2}$f($\frac{x}{2}$-1)=$\frac{1}{2}$×2(1-|$\frac{x}{4}$-$\frac{5}{2}$|)=1-|$\frac{x}{4}$-$\frac{5}{2}$|,
由g(x)=f(x)-logax=0,得f(x)=logax,分别作出函数f(x)和y=logax的图象,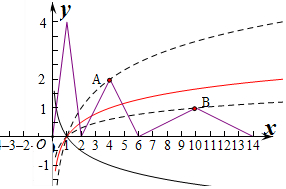
若0<a<1,则此时两个函数图象只有1个交点,不满足条件.
若a>1,当对数函数图象经过A时,两个图象只有2个交点,当图象经过点B时,两个函数有4个交点,
则要使两个函数有3个交点,则对数函数图象必须在A点以下,B点以上,
∵f(4)=2,f(10)=1,∴A(4,2),B(10,1),
即满足$\left\{\begin{array}{l}{lo{g}_{a}4<f(4)}\\{lo{g}_{a}10>f(10)}\end{array}\right.$,
即$\left\{\begin{array}{l}{lo{g}_{a}4<2}\\{lo{g}_{a}10>1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}>4}\\{a<10}\end{array}\right.$,
即2<a<10,
故选:C.
点评 本题主要考查分段函数的应用,利用函数零点和方程之间的关系,将条件转化为两个函数交点问题,利用数形结合是解决本题的关键.综合性较强,有一点的难度.

| A. | p∧q | B. | (¬p)∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
| A. | 405 | B. | 810 | C. | 243 | D. | 64 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{3}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | k≥4 | B. | k>4 | C. | k≥8 | D. | k>8 |