题目内容

16．已知集合A={x∈N|1＜x＜log2k}，集合A中至少有2个元素，则（　　）
A．k≥4B．k＞4C．k≥8D．k＞8

分析 首先确定集合A，由此得到log2k＞3，由此求得k的取值范围．

解答 解：∵集合A={x∈N|1＜x＜log2k}，集合A中至少有2个元素，
∴A={2，3}，
∴log2k＞3，
∴k＞8．
故选：D．

点评 本题考查了集合的化简与应用，属于基础题．

练习册系列答案
相关题目
6．已知数列{an}满足an+2=$\left\{\begin{array}{l}{{a}_{n}+2，n为奇数}\\{2{a}_{n}，n为偶数}\end{array}\right.$，n∈N*，且a1=1，a2=2．
（1）求数列{an}的通项公式；
（2）令bn=（-1）nanan+1，n∈N*，求数列{bn}的前n项和Sn．
7．定义在R上的函数y=f（x），当x∈[0，2]时，f（x）=4（1-|x-1|），且对任意实数x∈[2n-2，2n+1-2]（n∈N*，n≥2），都有f（x）=$\frac{1}{2}$f（$\frac{x}{2}$-1）．若g（x）=f（x）-logax有且仅有3个零点，则实数a的取值范围是（　　）
A．[2，10]B．[$\sqrt{2}$，$\sqrt{10}$]C．（2，10）D．[2，10）
4．设△ABC的内角A、B、C所对的边分别为a、b、c，若a2sinC=4sinA，cosB=$\frac{\sqrt{7}}{4}$，则△ABC的面积为（　　）
A．1B．$\frac{3}{2}$C．2D．$\frac{5}{2}$
11．已知向量$\overrightarrow{a}$=（sinx，mcosx），$\overrightarrow{b}$=（3，-1）．
（1）若$\overrightarrow{a}$∥$\overrightarrow{b}$，且m=1，求2sin2x-3cos2x的值；
（2）若函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$的图象关于直线x=$\frac{2π}{3}$对称，求函数f（2x）在[$\frac{π}{8}$，$\frac{2π}{3}$]上的值域．
1．已知点O为△ABC的外心，且$|{\overrightarrow{BA}}|=2，|{\overrightarrow{BC}}|=6$，则$\overrightarrow{BO}•\overrightarrow{AC}$=（　　）
A．-32B．-16C．32D．16
8．若数列{an}是公差为2的等差数列，数列{bn}满足b1=1，b2=2且anbn+bn=nbn+1．
（1）求数列{an}、{bn}的通项公式；
（2）设数列{cn}满足cn=$\frac{{a}_{n}+1}{{b}_{n+1}}$，数列{cn}的前n项和为Tn，则Tn＜4．
5．双曲线的焦点到渐近线的距离等于半实轴长，则该双曲线的离心率等于（　　）
A．$\sqrt{2}$B．$\sqrt{3}$C．2D．3
6．执行如图的程序框图，若输入k的值为3，则输出S的值为（　　）
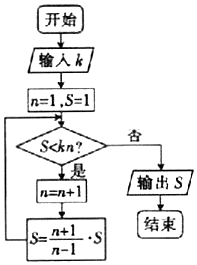
A．10B．15C．18D．21

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网