题目内容
已知平面α∩平面β=L，点A∈α，点B∈β，A∉L，B∉L．求证L与AB是异面直线．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：利用反证法证明．
解答：
解：假设L与AB不是异面直线，
那么它们在同一个平面上，记这个平面为p．
∵A和L都在p上，∴由它们决定的平面α在平面p上，
∴平面p=平面a．同理p=平面β．
∴α=β，∵A∈α，∴A∈β，
所以A在α与β的交线L上，矛盾．
∴假设不成立，
∴L与AB是异面直线．
那么它们在同一个平面上，记这个平面为p．
∵A和L都在p上，∴由它们决定的平面α在平面p上，
∴平面p=平面a．同理p=平面β．
∴α=β，∵A∈α，∴A∈β，
所以A在α与β的交线L上，矛盾．
∴假设不成立，
∴L与AB是异面直线．
点评：本题考查两条直线是异面直线的证明，是基础题，解题时要注意反证法的灵活运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
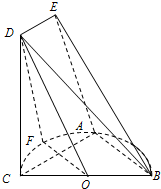如图：已知BC是半径为1的半圆O的直径，A是半圆周上不同于B，C的点，F为弧AC的中点．在梯形ACDE中，DE∥AC且AC=2DE，平面ACDE⊥平面ABC．求证：