题目内容
请画出函数y=丨x2-2丨的图象，并求单调区间．
考点：函数的图象
专题：函数的性质及应用
分析：先画出二次函数y=x2-2 的图象，再把图象位于x轴下方的部分关于x轴对称到x轴的上方，即可得到函数y=|x2-2|的图象．
解答：
解：先画出二次函数y=x2-2 的图象，再把图象位于x轴下方的部分关于x轴对称到x轴的上方，
即可得到函数y=|x2-2|的图象，如图（红线部分）所示：
由图象可知：函数的单调增区间：（-
，0]，（
，+∞）．
单调减区间：（-∞，-
]，（0，
]．：
解：先画出二次函数y=x2-2 的图象，再把图象位于x轴下方的部分关于x轴对称到x轴的上方，即可得到函数y=|x2-2|的图象，如图（红线部分）所示：
由图象可知：函数的单调增区间：（-
| 2 |
| 2 |
单调减区间：（-∞，-
| 2 |
| 2 |
点评：本题主要考查二次函数的图象和性质，函数的图象的对称性，属于基础题．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
已知l，m是两条不同的直线，α是一个平面，以下命题正确的是（ ）
| A、若l⊥α，l⊥m，则m?α |
| B、若l∥α，m?α，则 l∥m |
| C、若l⊥α，m∥α，则 l⊥m |
| D、若l⊥α，l⊥m，则 m∥α |
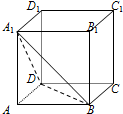如图，正方体ABCD-A1B1C1D1中