题目内容
生产方提供50箱的一批产品,其中有2箱不合格产品.采购方接收该批产品的准则是:从该批产品中任取5箱产品进行检测,若至多有1箱不合格产品,便接收该批产品.问:该批产品被接收的概率是多少?
考点:超几何分布的应用
专题:计算题,概率与统计
分析:以50箱为一批产品,从中随机抽取5箱,用X表示“5箱中不合格产品的箱数”,则X服从超几何分布H(5,2,50),即可得出结论.
解答:
解:以50箱为一批产品,从中随机抽取5箱,用X表示“5箱中不合格产品的箱数”,则X服从超几何分布H(5,2,50).
这批产品被接收的条件是5箱中没有不合格的箱或只有1箱不合格,
所以被接收的概率为P(X≤1),即P(X≤1)=
+
=
.
答:该批产品被接收的概率是
.
这批产品被接收的条件是5箱中没有不合格的箱或只有1箱不合格,
所以被接收的概率为P(X≤1),即P(X≤1)=
| ||||
|
| ||||
|
| 243 |
| 245 |
答:该批产品被接收的概率是
| 243 |
| 245 |
点评:注意二项分布和超几何分布的性质和应用.

练习册系列答案
相关题目
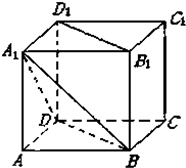 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中,