题目内容
设数列{bn}满足bn=(-2n)•(
)n-1,求该数列的前n项和Tn.
| 1 |
| 2 |
考点:数列的求和
专题:计算题,等差数列与等比数列
分析:这是等差数列乘等比数列型的求和,运用错位相减法即可,先写出Tn,再两边乘公比,再相减,注意错位,再由等比数列求和公式,化简即得.
解答:
解:∵bn=(-2n)•(
)n-1=-n(
)n-2,
∴Tn=-1×(
)-1-2×(
)0-…-n•(
)n-2,
∴-Tn=1×(
)-1+2×(
)0+…+n•(
)n-2,
-
Tn=1×(
)0+2×(
)1+…+(n-1)•(
)n-2+n•(
)n-1,
∴两式相减得,-
Tn=(
)-1+(
)0+(
)1+…+(
)n-2-n•(
)n-1,
=
-n•(
)n-1
=4-(
)n-2-n•(
)n-1
∴Tn=(
)n-3+n(
)n-2-8=(n+2)•(
)n-2-8.
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=-1×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴-Tn=1×(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴两式相减得,-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
2[1-(
| ||
1-
|
| 1 |
| 2 |
=4-(
| 1 |
| 2 |
| 1 |
| 2 |
∴Tn=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查数列求和的方法:错位相减法,注意解题步骤,属于基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
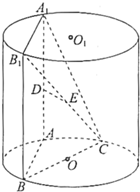 如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.
如图,AA1、BB1为圆柱OO1的母线(母线与底面垂直),BC是底面圆O的直径,D、E分别是AA1、CB1的中点,DE⊥平面CBB1.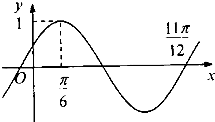 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|