题目内容
顶点在坐标原点的抛物线C以双曲线
-
=1的左准线l为准线,F为抛物线C的焦点,过F的直线交抛物线于A,B两点,且|AF|>|BF|.
﹙1)求抛物线C的方程;
(2)若直线AB的倾斜角为
,求AF的长.
| x2 |
| 12 |
| y2 |
| 4 |
﹙1)求抛物线C的方程;
(2)若直线AB的倾斜角为
| π |
| 3 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出抛物线C的准线为x=-3,由此能求出抛物线C的方程为y2=12x.
(2)直线AB的方程为:y=
(x-3),由
,得x2-10x+9=0,由此能求出AF的长.
(2)直线AB的方程为:y=
| 3 |
|
解答:
解:(1)∵双曲线
-
=1的左准线l为x=-
=-3,
∴抛物线C的准线为x=-3,
设抛物线方程为y2=2px,p>0,
∴-
=-3,解得p=6,
∴抛物线C的方程为y2=12x.
(2)∵过F(3,0)的直线交抛物线于A,B两点,且|AF|>|BF|,
直线AB的倾斜角为
,
∴直线AB的方程为:y=
(x-3),
由
,得x2-10x+9=0,
解得
,或
,
∵
=4,
=2
.
∴AF的长为2
.
| x2 |
| 12 |
| y2 |
| 4 |
| 12 | ||
|
∴抛物线C的准线为x=-3,
设抛物线方程为y2=2px,p>0,
∴-
| p |
| 2 |
∴抛物线C的方程为y2=12x.
(2)∵过F(3,0)的直线交抛物线于A,B两点,且|AF|>|BF|,
直线AB的倾斜角为
| π |
| 3 |
∴直线AB的方程为:y=
| 3 |
由
|
解得
|
|
∵
(3-1)2+(-2
|
(9-1)2+(6
|
| 43 |
∴AF的长为2
| 43 |
点评:本题考查抛物线方程的求法,考查线段长的求法,是中档题,解题时要注意两点间距离公式的合理运用.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
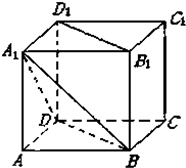 在正方体ABCD-A1B1C1D1中,
在正方体ABCD-A1B1C1D1中, 如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为
如图所示,一个空间几何的主视图和左视图都是边长为2的正方形,俯视图是一个直径为2的圆,那么这个几何体的体积为