题目内容
设函数f(x)=4sin(3x+1)-x,则下列区间中f(x)不存在零点的是( )
| A、[0,1] |
| B、[-2,-1] |
| C、[3,4] |
| D、[-3,-2] |
考点:正弦函数的图象
专题:函数的性质及应用,三角函数的求值,三角函数的图像与性质
分析:首先求出利用函数f(x)=4sin(3x+1)-x,求出f(3)的范围,进一步求出f(4)的范围,最后利用f(3)•f(4)>0说明在(3,4)上不存在零点.
解答:
解:已知函数f(x)=4sin(3x+1)-x,由于sin10<0
所以:f(3)=4sin10-3<0
又因为:0<sin13<1
所以:f(4)=4sin13-4<0
所以f(3)•f(4)>0
所以:在(3,4)上不存在零点.
故选:C
所以:f(3)=4sin10-3<0
又因为:0<sin13<1
所以:f(4)=4sin13-4<0
所以f(3)•f(4)>0
所以:在(3,4)上不存在零点.
故选:C
点评:本题考查的知识要点:三角函数的值域,及函数零点的应用,属于基础题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
曲线y=2x-x3在x=-1处的切线方程为( )
| A、x-y+2=0 |
| B、x+y-2=0 |
| C、x+y+2=0 |
| D、x-y-2=0 |
若-9、a、-l成等差数列,-9、m、b、n、-1成等比数列,则ab=( )
| A、15 | B、-l5 |
| C、±l5 | D、10 |
下列函数为周期函数的是( )
| A、f(x)=sinx,x∈[0,2π] | ||
B、f(x)=
| ||
| C、f(x)=sin|x| | ||
| D、f(x)=2014(x∈Z) |
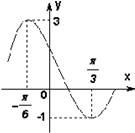 已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<
已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|< 已知函数f(x)为奇函数,当x≥0时,f(x)=
已知函数f(x)为奇函数,当x≥0时,f(x)=