题目内容
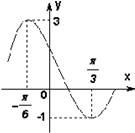 已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<
已知三角函数f(x)=Acos(ωx+φ)+b(A>ω>0,|φ|<| π |
| 2 |
(1)求函数的解析式;
(2)若函数g(x)=f(x-
| π |
| 6 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值
专题:三角函数的图像与性质
分析:(1)由题知A+b=3,-A+b=-1,
=
-(-
)=
,即可求得A,b,ω,φ的值,从而可求函数的解析式;
(2)由已知化简得g(x)=4(cosx+
)2-2可求当cosx=1时,有g(x)max=7;当cosx=-
时,有g(x)min=-2,于是可求函数g(x)在x∈[0,π]上的值域.
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
(2)由已知化简得g(x)=4(cosx+
| 1 |
| 2 |
| 1 |
| 2 |
解答:

(1)由题知A+b=3,-A+b=-1,
=
-(-
)=
,
所以A=2,b=1,ω=
=2,又f(
)=-1得φ=
所以函数的解析式:f(x)=2cos(2x+
)+1…(6分)
(2)g(x)=f(x-
)+4cosx=2cos2x+1+4cosx
=4cos2x+4cosx-1
=4(cosx+
)2-2 …(9分)
因x∈[0,π]时,cosx∈[-1,1],从而当cosx=1时,有g(x)max=4(1+
)2-2=7;当cosx=-
时,
有g(x)min=-2,于是函数g(x)在x∈[0,π]上的值域为[-2,7]…(12分)

(1)由题知A+b=3,-A+b=-1,
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以A=2,b=1,ω=
| 2π |
| T |
| π |
| 3 |
| π |
| 3 |
所以函数的解析式:f(x)=2cos(2x+
| π |
| 3 |
(2)g(x)=f(x-
| π |
| 6 |
=4cos2x+4cosx-1
=4(cosx+
| 1 |
| 2 |
因x∈[0,π]时,cosx∈[-1,1],从而当cosx=1时,有g(x)max=4(1+
| 1 |
| 2 |
| 1 |
| 2 |
有g(x)min=-2,于是函数g(x)在x∈[0,π]上的值域为[-2,7]…(12分)
点评:本题主要考察了由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值的求法,属于中档题.

练习册系列答案
相关题目
已知2∈{1,a,a-1},则实数a的值为( )
| A、2 | B、3 | C、2或3 | D、无解 |
设函数f(x)=4sin(3x+1)-x,则下列区间中f(x)不存在零点的是( )
| A、[0,1] |
| B、[-2,-1] |
| C、[3,4] |
| D、[-3,-2] |
已知
=(1,2),
=(3,-1),若λ
+
与
垂直,则λ=( )
| a |
| b |
| a |
| b |
| b |
| A、-10 | B、10 | C、-2 | D、2 |
已知函数g(x)=(
)x与函数y=f(x)的图象关于直线y=x对称,若a=g(0.2),b=f(2),c=f(0.2),则( )
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、a<c<b |
| D、c<b<a |
阅读程序框图,运行相应的程序,输出的结果为( )
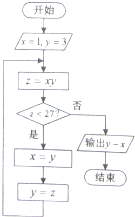

| A、6 | B、-6 | C、0 | D、18 |