题目内容
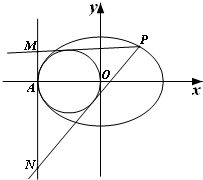如图，离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
（Ⅰ）求椭圆的方程；
（Ⅱ）若OA是圆C的直径，P（x0，y0）（x0＞0）为椭圆上的动点，过P作圆C的两条切线，分别交直线l于点M、N，求当
| PM |
| PN |
考点：直线与圆锥曲线的关系,椭圆的标准方程
专题：综合题,圆锥曲线的定义、性质与方程
分析：（Ⅰ）由题：a=2，利用离心率为
，求出c，从而可求b，即可求椭圆的方程；
（Ⅱ）切线PM、PN的斜率均存在，设为k1、k2，利用直线PM、PN与圆C相切，可得k1、k2是关于k的方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个根，利用向量表示出
•
，构建函数，利用函数的性质，即可求当
•
取得最小值时P点的横坐标x0．
| ||
| 2 |
（Ⅱ）切线PM、PN的斜率均存在，设为k1、k2，利用直线PM、PN与圆C相切，可得k1、k2是关于k的方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个根，利用向量表示出
| PM |
| PN |
| PM |
| PN |
解答：
解：（Ⅰ）由题：a=2，又e=
=
，∴c=
，从而b=
∴椭圆的方程为
+
=1． …．（4分）
（Ⅱ）由题意，圆C的方程为（x+1）2+y2=1．
∵x0＞0，∴切线PM、PN的斜率均存在，设为k1、k2，
则直线PM：y-y0=k1（x-x0），
由其与圆C相切得：
=1，…（6分）
化简得：(x02+2x0)k12-2y0(x0+1)k1+y02-1=0
同理：(x02+2x0)k22-2y0(x0+1)k2+y02-1=0
∴k1、k2是关于k的方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个根△=[-2y0(x0+1)]2-4(x02+2x0)(y02-1)=4(x02+2x0+y02)＞0恒成立．
k1+k2=
，k1k2=
，…．（9分）
M（-2，y0-（2+x0）k1），N（-2，y0-（2+x0）k2），
∴
=(-2-x0，-（2+x0）k1），
=(-2-x0，-（2+x0）k2），
∴
•
=(2+x0)2+(2+x0)2k1k2=(2+x0)2[1+
]=
=f（x0）…．（12分）
f′(x0)=
=
(x0+
+1)(x0-
+1)，x0∈（0，2]
∴f（x0）在（0，
-1)上单调递减，在(
-1，2]上单调递增，
∴当x0=
-1时，f（x0）取得最小值，即
•
取得最小值． …．（14分）
| c |
| a |
| ||
| 2 |
| 2 |
| 2 |
∴椭圆的方程为
| x2 |
| 4 |
| y2 |
| 2 |
（Ⅱ）由题意，圆C的方程为（x+1）2+y2=1．
∵x0＞0，∴切线PM、PN的斜率均存在，设为k1、k2，
则直线PM：y-y0=k1（x-x0），
由其与圆C相切得：
| |(x0+1)k1-y0| | ||
|
化简得：(x02+2x0)k12-2y0(x0+1)k1+y02-1=0
同理：(x02+2x0)k22-2y0(x0+1)k2+y02-1=0
∴k1、k2是关于k的方程(x02+2x0)k2-2y0(x0+1)k+y02-1=0的两个根△=[-2y0(x0+1)]2-4(x02+2x0)(y02-1)=4(x02+2x0+y02)＞0恒成立．
k1+k2=
| 2y0(x0+1) |
| x02+2x0 |
| y02-1 |
| x02+2x0 |
M（-2，y0-（2+x0）k1），N（-2，y0-（2+x0）k2），
∴
| PM |
| PN |
∴
| PM |
| PN |
| y02-1 |
| x02+2x0 |
| (x0+2)(x02+4x0+2) |
| 2x0 |
f′(x0)=
| x03+3x02-2 |
| x02 |
| x0+1 |
| x02 |
| 3 |
| 3 |
∴f（x0）在（0，
| 3 |
| 3 |
∴当x0=
| 3 |
| PM |
| PN |
点评：本题考查椭圆的方程，考查直线与圆、椭圆的位置关系，考查向量知识的运用，综合性强．
练习册系列答案
相关题目
如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．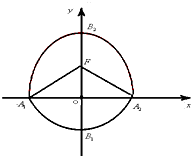
如图，曲线C由半椭圆