题目内容
已知椭圆
+
=1(a>b>0)的左右顶点分别为A(-2,0),B(2,0),离心率e=
.
(1)求椭圆的标准方程;
(2)若M,N是该椭圆上关于原点对称的点,M,N异于B点,直线MB与直线NB的斜率分别为K1,k2,计算K1•k2的值;
(3)若直线MB,直线NB分别与直线x=6相交C,D两点,证明以CD为直径的圆恒经过定点,并且求定点坐标.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆的标准方程;
(2)若M,N是该椭圆上关于原点对称的点,M,N异于B点,直线MB与直线NB的斜率分别为K1,k2,计算K1•k2的值;
(3)若直线MB,直线NB分别与直线x=6相交C,D两点,证明以CD为直径的圆恒经过定点,并且求定点坐标.
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出
,由此能求出椭圆的标准方程.
(2)设M(x1,y1),B(x0,y0),则N(-x1,-y1),由此能求出k1k2=
•
=
=-
.
(3)假设x1>0,y1>0,直线BM:
=
,把x=6代入,得:C(6,
),直线BN:
=
,把x=6代入,得:D(6,
),由此求出以CD为直径的圆的圆心O(6,-
),半径r=
|CD|=
,从而能够证明以CD为直径的圆恒经过定点,定点坐标为(4,0).
|
(2)设M(x1,y1),B(x0,y0),则N(-x1,-y1),由此能求出k1k2=
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
| y02-y12 |
| x02-x02 |
| 1 |
| 4 |
(3)假设x1>0,y1>0,直线BM:
| y |
| x-2 |
| y1 |
| x1-2 |
| 4y1 |
| x1-2 |
| y |
| x-2 |
| -y1 |
| -x1-2 |
| 4y1 |
| x1+2 |
| x1 |
| y1 |
| 1 |
| 2 |
| 2 |
| y1 |
解答:
(1)解:∵椭圆
+
=1(a>b>0)的左右顶点
分别为A(-2,0),B(2,0),离心率e=
,
∴
,解得a=2,c=
,b2=4-3=1,
∴椭圆的标准方程为
+y2=1.
(2)解:设M(x1,y1),B(x0,y0),
∵M,N是该椭圆上关于原点对称的点,M,N异于B点,
∴N(-x1,-y1),|x1|≠|x0|,
∴k1=
,k2=
,
k1k2=
•
=
,
∵M(x1,y1),B(x0,y0)都是椭圆
+y2=1上的点,
∴
,两式相减,得:
+(y02-y12)=0,
∴k1k2=
=-
.
(3)证明:假设x1>0,y1>0,直线BM:
=
,把x=6代入,得:C(6,
),
直线BN:
=
,把x=6代入,得:D(6,
),
∴|CD|=
-
=
=
=
,
∵
(
+
)=
+
=
=
=-
,
∴以CD为直径的圆的圆心O(6,-
),半径r=
|CD|=
,
∵点(4,0)到圆心O(6,-
)的距离:
d=
=
=
=
=r,
∴以CD为直径的圆恒经过定点,定点坐标为(4,0).
| x2 |
| a2 |
| y2 |
| b2 |
分别为A(-2,0),B(2,0),离心率e=
| ||
| 2 |
∴
|
| 3 |
∴椭圆的标准方程为
| x2 |
| 4 |
(2)解:设M(x1,y1),B(x0,y0),
∵M,N是该椭圆上关于原点对称的点,M,N异于B点,
∴N(-x1,-y1),|x1|≠|x0|,
∴k1=
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
k1k2=
| y0-y1 |
| x0-x1 |
| y0+y1 |
| x0+x1 |
| y02-y12 |
| x02-x02 |
∵M(x1,y1),B(x0,y0)都是椭圆
| x2 |
| 4 |
∴
|
| x02-x12 |
| 4 |
∴k1k2=
| y02-y12 |
| x02-x02 |
| 1 |
| 4 |
(3)证明:假设x1>0,y1>0,直线BM:
| y |
| x-2 |
| y1 |
| x1-2 |
| 4y1 |
| x1-2 |
直线BN:
| y |
| x-2 |
| -y1 |
| -x1-2 |
| 4y1 |
| x1+2 |
∴|CD|=
| 4y1 |
| x1+2 |
| 4y1 |
| x1-2 |
| -16y1 |
| x12-4 |
| -16y1 |
| -4y12 |
| 4 |
| y1 |
∵
| 1 |
| 2 |
| 4y1 |
| x1-2 |
| 4y1 |
| x1+2 |
| 2y1 |
| x1-2 |
| 2y1 |
| x1+2 |
| 4x1y1 |
| x12-2 |
| 4x1y1 |
| -4y12 |
| x1 |
| y1 |
∴以CD为直径的圆的圆心O(6,-
| x1 |
| y1 |
| 1 |
| 2 |
| 2 |
| y1 |
∵点(4,0)到圆心O(6,-
| x1 |
| y1 |
d=
(6-4)2+(-
|
4+
|
|
| 2 |
| y1 |
∴以CD为直径的圆恒经过定点,定点坐标为(4,0).
点评:本题考查椭圆方程的求法,考查两直线斜率乘积的求法,考查圆过定点的证明,解题时要认真审题,注意两点间距离公式的合理运用.

练习册系列答案
相关题目
 已知圆O:x2+y2=4.
已知圆O:x2+y2=4. 如图,离心率为
如图,离心率为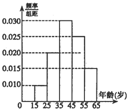 某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示:
某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样了n人,回答问题统计结果如图表所示: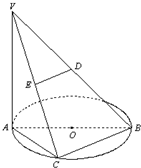 如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.
如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.