题目内容
若函数f(x)=
+
(a为常数),对于定义域内的任意两个实数x1、x2,恒有|f(x1)-f(x2)|<1成立,用S(a)表示满足条件的所有正整数a的和,则S(a)= .
| a-x |
| x |
考点:函数恒成立问题
专题:函数的性质及应用
分析:利用三角函数换元法,求出函数f(x)的最大值和最小值,即可得到结论.
解答:
解:设
=
cosθ,则
=
sinθ,θ∈[0,
],
则f(x)=
+
=
sinθ+
cosθ=
sin(θ+
),
∵0≤θ≤
,
∴
≤θ+
≤
,
∴fmax(x)=
,fmin(x)=
,
要使对于定义域内的任意两个实数x1、x2,恒有|f(x1)-f(x2)|<1,
则
-
=(
-1)•
<1,
即
<
,
∴a<3+2
,
∵a为正整数,
∴a=1,2,3,4,5,
则s(a)=1+2+3+4+5=15,
故答案为:15
| x |
| a |
| a-x |
| a |
| π |
| 2 |
则f(x)=
| a-x |
| x |
| a |
| a |
| 2a |
| π |
| 4 |
∵0≤θ≤
| π |
| 2 |
∴
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
∴fmax(x)=
| 2a |
| a |
要使对于定义域内的任意两个实数x1、x2,恒有|f(x1)-f(x2)|<1,
则
| 2a |
| a |
| 2 |
| a |
即
| a |
| 1 | ||
|
∴a<3+2
| 2 |
∵a为正整数,
∴a=1,2,3,4,5,
则s(a)=1+2+3+4+5=15,
故答案为:15
点评:本题主要考查函数恒成立问题,利用三角换元法将函数转化,求出函数的最值是解决本题的关键.

练习册系列答案
相关题目
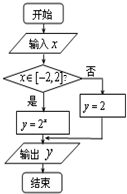
阅读程序框图(如图),如果输出的函数值在区间[
,1]上,则输入的实数x的取值范围是( )
| 1 |
| 4 |

| A、(-∞,-2] |
| B、[-2,0] |
| C、[0,2] |
| D、[2,+∞) |
 已知数列{an}中,a1=1,an+1=2an+n-1,若利用如图所示的程序框图进行运算,则输出n的值为
已知数列{an}中,a1=1,an+1=2an+n-1,若利用如图所示的程序框图进行运算,则输出n的值为