题目内容
设函数f（x）=
，则是否存在实数a，使得至少有一个正实数b，使函数f（x）的定义域和值域相同？若存在，求出a的值；若不存在，请说明理由．
| ax2+bx |
考点：函数的值域,函数的定义域及其求法
专题：分类讨论,函数的性质及应用
分析：把根号里面的式子看成关于x的二次函数，由于二次项前面的系数含有参数，所以它的定义域和值域，都与a有关，即要分三类情况进行分类讨论．
解答：
解：存在．∵b＞0，
①当 a＞0时，定义域是包含x=-
＜0，值域是f（x）≥0，不可能相等；
②当 a=0时，定义域是x≥0，值域也是f（x）≥0，符合题意；
③当a＜0时，定义域是[0，-
]，值域是[0，
]相同就有-
=
，解得a=-4；
综合以上得：a=0或a=-4时函数f（x）的定义域和值域相同．
①当 a＞0时，定义域是包含x=-
| b |
| a |
②当 a=0时，定义域是x≥0，值域也是f（x）≥0，符合题意；
③当a＜0时，定义域是[0，-
| b |
| a |
|
| b |
| a |
|
综合以上得：a=0或a=-4时函数f（x）的定义域和值域相同．
点评：本题是考查二次函数的定义和值域问题，这里要对参数a进行分类讨论，分小于零，等于零各大于零三类．
练习册系列答案
相关题目
已知f（x）是定义在R上的奇函数，且在（0，+∞）内有1006个零点，则f（x）的零点共有（ ）
| A、1006个 |
| B、1007个 |
| C、2012个 |
| D、2013个 |
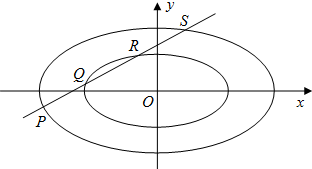（理）已知中心在原点O，左焦点为F1（-1，0）的椭圆C1的左顶点为A，上顶点为B，F1到直线AB的距离为