题目内容
设不等式组
表示的区域为Ω1,不等式x2+y2≤1表示的平面区域为Ω2.
(1)若Ω1与Ω2有且只有一个公共点,则a= ;
(2)记S(a)为Ω1与Ω2公共部分的面积,则函数S(a)的取值范围是 .
|
(1)若Ω1与Ω2有且只有一个公共点,则a=
(2)记S(a)为Ω1与Ω2公共部分的面积,则函数S(a)的取值范围是
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)作出不等式组对应的平面区域,利用Ω1与Ω2有且只有一个公共点,确定直线的位置即可得到结论;
(2)作出Ω1与Ω2对应的平面区域,利用数形结合即可得到结论.
(2)作出Ω1与Ω2对应的平面区域,利用数形结合即可得到结论.
解答:
解:(1)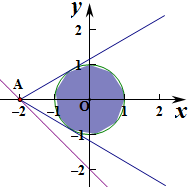 作出不等式组对应的平面区域,若Ω1与Ω2有且只有一个公共点,
作出不等式组对应的平面区域,若Ω1与Ω2有且只有一个公共点,
则圆心O到直线x+ay+2=0的距离d=1,
即
=1,即a2=3,解得a=±
.
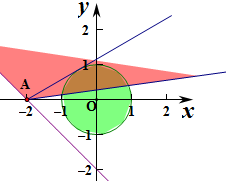
(2)当不等式x2+y2≤1表示的平面区域为Ω2.
若a=0时,Ω1与Ω2公共部分的区域面积最小为0,
当a>0时,不等式组
对应的平面区域在圆的下方,此时Ω1与Ω2公共部分的区域最大为半圆,面积为
×π×12=
;

若a<0,不等式组
对应的平面区域在圆的上方,此时Ω1与Ω2公共部分的区域最大为半圆,面积为
×π×12=
;
总上S(a)∈[0,
),
故答案为:±
,[0,
).
 作出不等式组对应的平面区域,若Ω1与Ω2有且只有一个公共点,
作出不等式组对应的平面区域,若Ω1与Ω2有且只有一个公共点,则圆心O到直线x+ay+2=0的距离d=1,
即
| 2 | ||
|
| 3 |
(2)当不等式x2+y2≤1表示的平面区域为Ω2.
若a=0时,Ω1与Ω2公共部分的区域面积最小为0,
当a>0时,不等式组
|
| 1 |
| 2 |
| π |
| 2 |

若a<0,不等式组
|
| 1 |
| 2 |
| π |
| 2 |

总上S(a)∈[0,
| π |
| 2 |
故答案为:±
| 3 |
| π |
| 2 |
点评:本题主要考查线性规划的应用,利用直线和圆的位置关系是解决本题的关键,利用数形结合是解决本题的基本数学思想.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
某几何体的三视图如图所示,则该几何体的体积为( )
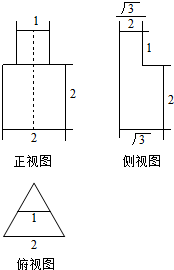

A、3
| ||||
B、
| ||||
C、
| ||||
D、
|
