题目内容
用符号“>,≥,<,≤”填空:
(1)
+
2(x,y∈R+);
(2)x+
-2(x<0);
(3)a+
2(a>1);
(4)(
)2
.
(1)
| x |
| y |
| y |
| x |
(2)x+
| 1 |
| x |
(3)a+
| 1 |
| a |
(4)(
| a+b |
| 2 |
| a2+b2 |
| 2 |
考点:不等式比较大小
专题:不等式的解法及应用
分析:根据基本不等式的性质,分别进行判断即可得到结论.
解答:
解:(1)根据基本不等式的性质可知
+
≥2
=2,当且仅当
=
,即x=y时,取等号.即
+
≥2,
(2)根据基本不等式的性质可知x+
=-(-x-
)≤-2
=-2,当且仅当-x=-
,即x=-1时,取等号;即x+
≤-2,
(3)∵a+
在a>1时,单调递增,∴a+
>1+1=2,即a+
>2,
(4)(
)2-
=-
=-
≤0,
∴(
)2≤
.
故答案为:≥,≤,>,≤
| x |
| y |
| y |
| x |
|
| x |
| y |
| y |
| x |
| x |
| y |
| y |
| x |
(2)根据基本不等式的性质可知x+
| 1 |
| x |
| 1 |
| x |
-x•
|
| 1 |
| x |
| 1 |
| x |
(3)∵a+
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
(4)(
| a+b |
| 2 |
| a2+b2 |
| 2 |
| a2-2ab+b2 |
| 4 |
| (a-b)2 |
| 4 |
∴(
| a+b |
| 2 |
| a2+b2 |
| 2 |
故答案为:≥,≤,>,≤
点评:本题主要考查不等式的大小判断,利用基本不等式是解决本题的关键,比较基础.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
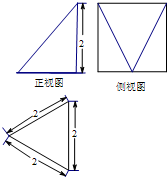
某几何体的三视图如图所示,则该几何体的体积是( )

A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|

