Question

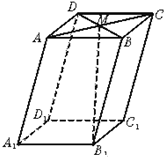如图，在平行六面体ABCD-A₁B₁C₁D₁中，M为AC与BD的交点．若

A1B1

=

a

，

A1D1

=

b

，

A1A

=

c

，则下列向量中与

B1M

相等的向量是（　　）

• A、-

  1

  2

  a

  +

  1

  2

  b

  +

  c

• B、

  1

  2

  a

  +

  1

  2

  b

  +

  c

• C、

  1

  2

  a

  -

  1

  2

  b

  +

  c

• D、-

  1

  2

  a

  -

  1

  2

  b

  +

  c

Answer 1

考点：空间向量运算的坐标表示

专题：空间向量及应用

分析：利用空间向量的加法运算法则求解．

解答： 解：由已知得：-

1

2

a

+

1

2

b

+

c

=

1

2

b

+

c

-

1

2

a

=

B1M

，故A正确；

1

2

a

+

1

2

b

+

c

=

A1M

，故B错误；

1

2

a

-

1

2

b

+

c

=

D1M

，故C错误；
-

1

2

a

-

1

2

b

+

c

=

C1M

，故D错误．
故选：A．

点评：本题考查空间向量运算的应用，是基础题，解题时要注意加法运算法则的合理运用．