题目内容

在△ABC中，a=
2
，b=
3
，B=
π
3
，则A等于（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
4
或
3π
4
考点：正弦定理
专题：解三角形
分析：由正弦定理可得：sinA=
asinB
b
=
2
2
，由a=
2
＜b=
3
，根据三角形中大边对大角可得A为锐角，即可求得A的值．
解答： 解：由正弦定理可得：sinA=
asinB
b
=
2
×sin
π
3
3
=
2
2
，
∵a=
2
＜b=
3
，
∴A为锐角，
∴A=
π
4
．
故选：B．
点评：本题主要考查了正弦定理，三角形中大边对大角等知识的应用，属于基础题．
练习册系列答案
相关题目
某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历．假定该毕业生得到甲、乙、丙三个公司面试的概率分别为
2
3
、p1、p2，且三个公司是否让其面试是相互独立的．记X为该毕业生得到面试的公司个数．若P（X=3）=
1
6
，且E（X）=
5
3
，则p1+p2=
 
．
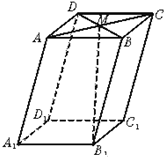如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点．若
A1B1
=
a
，
A1D1
=
b
，
A1A
=
c
，则下列向量中与
B1M
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、
1
2
a
-
1
2
b
+
c
D、-
1
2
a
-
1
2
b
+
c
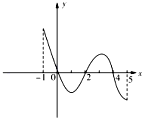已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．
x-10245
y12021
若函数y=f（x）-a有4个零点，则实数a的取值范围为（　　）
A、[1，2）
B、[1，2]
C、（2，3）
D、[1，3）
如图，某商业中心O有通往正东方向和北偏东30°方向的两条街道，某公园P位于商业中心北偏东θ角（0＜θ＜
π
2
，tanθ=3
3
），且与商业中心O的距离为
21
公里处，现要经过公园P修一条直路分别与两条街道交汇于A，B两处．
（1）当AB沿正北方向时，试求商业中心到A，B两处的距离和；
（2）若要使商业中心O到A，B两处的距离和最短，请确定A，B的最佳位置．
从2007名学生中选取50名学生参加全国数学联赛，计划采用下面的方法选取：先用简单随机抽样从2007人中剔除7人，剩下的2000人再按系统抽样的方法抽取．则这种方法下，每人入选的概率（　　）
A、不全相等
B、均不相等
C、都相等，且为
1
40
D、都相等，且为
50
2007
计算：log318-log32+2log52•log25．
已知（
a
+
b
）⊥（
a
+3
b
），求证|
a
+2
b
|=|
b
|．
已知α是第二象限角，P（x，
5
）为其终边上一点，且cosα=
2
4
x，则x=（　　）
A、
3
B、±
3
C、-
2
D、-
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网