题目内容

已知|
a
|=2|
b
|=1，＜
a
，
b
＞=60°，向量2t
a
+7
b
与
a
+t
b
夹角为钝角，求t范围．
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：由题意可得（2t
a
+7
b
）•（
a
+t
b
）＜0 且2t
a
+7
b
与
a
+t
b
不共线，化简可得2t+（2t2+7）•
1
4
+7t•
1
4
＜0，且
2t
1
≠
7
t
，由此求得t的范围．
解答： 解：由题意可得
a
•
b
=1×
1
2
×cos60°=
1
4
，
a
2=1，
b
2=
1
4
，
由2t
a
+7
b
与
a
+t
b
夹角为钝角可得（2t
a
+7
b
）•（
a
+t
b
）＜0 且2t
a
+7
b
与
a
+t
b
不共线．
即2t+（2t2+7）•
1
4
+7t•
1
4
＜0，且
2t
1
≠
7
t
，
求得-2＜t＜-
1
2
，且 t≠±
14
2
，即-2＜t＜-
14
2
 或-
14
2
＜t＜-
1
2
．
点评：本题主要考查两个向量的数量积的定义，两个向量共线的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
在平面直角坐标系xoy中，已知点A（0，1），B点在直线y=-1上，M点满
MB
∥
OA
，
MA
•
AB
=
MB
•
BA
，M点的轨迹曲线C
（1）求曲线C的方程；
（2）斜率为1的直线l过原点O，求l被曲线C截得的弦长．
函数y=f（x）是定义域为R的奇函数，且对任意的x∈R，都有f（x+4）=f（x）成立，当x∈（0，2），f（x）=-x2+1．
（Ⅰ）当x∈（2，6）时，求函数f（x）的解析式；
（Ⅱ）求不等式f（x）＞-1在区间（2，6）上的解集．
若曲线x2-y2=1与曲线（x-1）2+y2=a2（a＞0）恰好有三个不同的公共点，则实数a的取值（范围）为
 
．
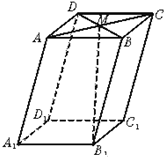如图，在平行六面体ABCD-A1B1C1D1中，M为AC与BD的交点．若
A1B1
=
a
，
A1D1
=
b
，
A1A
=
c
，则下列向量中与
B1M
相等的向量是（　　）
A、-
1
2
a
+
1
2
b
+
c
B、
1
2
a
+
1
2
b
+
c
C、
1
2
a
-
1
2
b
+
c
D、-
1
2
a
-
1
2
b
+
c
已知圆C的方程：x2+y2-2x-4y+m=0．
（1）求m的取值范围；
（2）当m=4时，求直线l：x+2y-4=0被圆C所截得的弦MN的长．
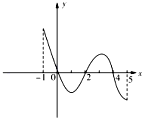已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．
x-10245
y12021
若函数y=f（x）-a有4个零点，则实数a的取值范围为（　　）
A、[1，2）
B、[1，2]
C、（2，3）
D、[1，3）
从2007名学生中选取50名学生参加全国数学联赛，计划采用下面的方法选取：先用简单随机抽样从2007人中剔除7人，剩下的2000人再按系统抽样的方法抽取．则这种方法下，每人入选的概率（　　）
A、不全相等
B、均不相等
C、都相等，且为
1
40
D、都相等，且为
50
2007
若书架上有中文书5本，英文书3本，日文书2本，则随机抽取一本恰为外文书的概率为（　　）
A、
1
2
B、
2
5
C、
3
10
D、
1
5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网