题目内容
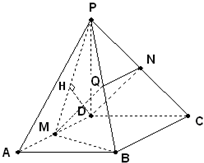
 已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.
已知四棱锥P-ABCD,底面ABCD是∠A=60°、边长为a的菱形,又PD⊥底ABCD,且PD=CD,点M、N分别是棱AD、PC的中点.(1)证明:MB⊥平面PAD;
(2)求点A到平面PMB的距离.
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)由已知条件推导出PD⊥MB,MB⊥AD.由此能证明MB⊥平面PAD.
(2)过点D作DH⊥PM于H,由已知条件推导出DH是点D到平面PMB的距离.由此能求出点A到平面PMB的距离.
(2)过点D作DH⊥PM于H,由已知条件推导出DH是点D到平面PMB的距离.由此能求出点A到平面PMB的距离.
解答:
 (1)证明:∵PD⊥平面ABCD,MB?平面ABCD,
(1)证明:∵PD⊥平面ABCD,MB?平面ABCD,
∴PD⊥MB,
又∵底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,
∴MB⊥AD.又AD∩PD=D,∴MB⊥平面PAD.
(2)解:∵M是AD中点,∴点A与D到平面PMB等距离.
过点D作DH⊥PM于H,
∵平面PMB⊥平面PAD,∴DH⊥平面PMB.
∴DH是点D到平面PMB的距离.
∵DH=
=
a.
∴点A到平面PMB的距离为
a.
 (1)证明:∵PD⊥平面ABCD,MB?平面ABCD,
(1)证明:∵PD⊥平面ABCD,MB?平面ABCD,∴PD⊥MB,
又∵底面ABCD是∠A=60°、边长为a的菱形,且M为AD中点,
∴MB⊥AD.又AD∩PD=D,∴MB⊥平面PAD.
(2)解:∵M是AD中点,∴点A与D到平面PMB等距离.
过点D作DH⊥PM于H,
∵平面PMB⊥平面PAD,∴DH⊥平面PMB.
∴DH是点D到平面PMB的距离.
∵DH=
| ||||
|
| ||
| 5 |
∴点A到平面PMB的距离为
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查点到平面的距离的求法,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
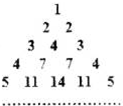 用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn.
用部分自然数构造如图的数表:用aij(i≥j)表示第i行第j个数(i,j∈N+),使得ai1=aij=i.每行中的其他各数分别等于其“肩膀”上的两个数之和.设第n(n∈N+)行中的各数之和为bn. 在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,
在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,