题目内容

如图中阴影部分区域的面积S=
 
．
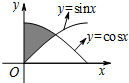
考点：定积分在求面积中的应用
专题：导数的概念及应用
分析：根据积分的应用，将阴影部分表示为积分函数即可得到结论．
解答： 解：由sinx=cosx得，x=
π
4
，
由积分的几何意义可知，阴影部分的面积
S=
∫
π
4
0
(cosx-sinx)dx=（sinx+cosx）
|
π
4
0
=sin
π
4
+cos
π
4
-（sin0+cos0）=
2
2
+
2
2
-1=
2
-1，
故答案为：
2
-1．
点评：本题主要考查积分的几何意义，利用积分即可确定阴影 部分的面积，要求熟练掌握常见函数的积分公式．
练习册系列答案
相关题目
已知a＞0且a≠1，f（x）=
a
a2-1
（ax-a-x）
（1）判断函数f（x）的奇偶性；
（2）判断函数f（x）的单调性，并证明；
（3）当函数f（x）的定义域为（-1，1）时，求使f（1-m）+f（1-m2）＜0成立的实数m的取值范围．
已知四棱锥P-ABCD，底面ABCD是∠A=60°、边长为a的菱形，又PD⊥底ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．
（1）证明：MB⊥平面PAD；
（2）求点A到平面PMB的距离．
已知程序框图如图所示，执行相应程序，输出y的值为1，则输入的整数x的值等于
 
．
关于曲线C：x4+y2=1，给出下列说法：
①关于坐标轴对称；      
②关于点（0，0）对称；
③关于直线y=x对称；  
④是封闭图形，面积大于π．
则其中正确说法的序号是
 
．（注：把你认为正确的序号都填上）
（1）若正数a，b满足ab=a+b+3，则分别求ab，a+b的取值范围
（2）若x＞0，求函数f（x）=
12
x
+3x的最小值；若x＜0，求函数f（x）=
12
x
+3x的值域．
已知函数f（x）=lnx+2x，若f（x2-4）＜2，则实数x的取值范围
 
．
给出下列四个命题：
①命题“?x∈R，cosx＞0”的否定是“?x∈R，cosx≤0”；
②若0＜a＜1，则函数f（x）=x2+ax-3只有一个零点；
③函数y=sin（2x-
π
3
）的一个单调增区间是[-
π
12
，
5π
12
]；
④对于任意实数x，有f（-x）=f（x），且当x＞0时，f′（x）＞0，则当x＜0时，f′（x）＜0．
⑤若m∈（0，1]，则函数y=m+
3
m
的最小值为2
3
；
其中真命题的序号是
 
（把所有真命题的序号都填上）．
在△ABC中，三边a，b，c所对的角分别为A，B，C，若a2-b2=
3
bc，sinC=2
3
sinB，则角A=（　　）
A、30°B、45°
C、150°D、135°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网