题目内容
已知函数f(x)=ln(ax)+(b-2)x(a,b是常数),此函数对应的曲线y=f(x)在点(1,-1)处的切线与直线x轴平行.
(Ⅰ)求a,b的值,并求f(x)的最大值;
(Ⅱ)设m≠0,函数g(x)=
mx3-mx,x∈(1,2),总存在x1∈(1,2),x2∈(1,2),使f(x1)-g(x2)=0,求实数m的取值范围.
(Ⅰ)求a,b的值,并求f(x)的最大值;
(Ⅱ)设m≠0,函数g(x)=
| 1 |
| 3 |
考点:利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求出函数的导数,由于曲线y=f(x)在点(1,-1)处的切线与直线x轴平行,则f′(1)=0,且f(1)=-1,解方程,即可得到a,b,再求出f(x)的地单调区间,进而得到极值,且为最值;
(Ⅱ)求出f(x)在(1,2)的值域,求出g(x)的导函数,讨论m>0,m<0,g(x)的单调性,求出值域,由于任意x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,则f(x)的值域包含在g(x)的值域,列出不等式,解出,再求并集即可.
(Ⅱ)求出f(x)在(1,2)的值域,求出g(x)的导函数,讨论m>0,m<0,g(x)的单调性,求出值域,由于任意x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,则f(x)的值域包含在g(x)的值域,列出不等式,解出,再求并集即可.
解答:
解:(Ⅰ)函数f(x)=ln(ax)+(b-2)x的导数为f′(x)=
+b-2,
由于曲线y=f(x)在点(1,-1)处的切线与直线x轴平行,
则f′(1)=0,且f(1)=-1,
即有1+b-2=0,且lna+b-2=-1,
解得,a=1,b=1;
则f(x)=lnx-x,(x>0),
f′(x)=
-1=
,
当x>1时,f′(x)<0,f(x)递减,
当0<xx<1时,f′(x)>0,f(x)递增,
则有f(x)在x=1处取得极大值,也为最大值,且为f(1)=-1;
(Ⅱ)f(x)在(1,2)递减,f(x)的值域为(ln2-2,-1),
g(x)的导数为g′(x)=mx2-m=m(x2-1),
当m>0时,g′(x)>0在(1,2)成立,g(x)递增,g(x)的值域为(-
m,
m);
当m<0时,g′(x)<0在(1,2)成立,g(x)递减,g(x)的值域为(
m,-
m).
任意x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,
则在(1,2)内,当m>0时,(ln2-2,-1)⊆(-
m,
m),
即有-
m≤ln2-2<-1≤
m,解得,m≥3-
ln2;
当m>0时,(ln2-2,-1)⊆(
m,-
m),
即有
m≤ln2-2<-1≤-
m,解得,m≤
ln2-3.
则m的取值范围是(-∞,
ln2-3]∪[3-
ln2,+∞).
| 1 |
| x |
由于曲线y=f(x)在点(1,-1)处的切线与直线x轴平行,
则f′(1)=0,且f(1)=-1,
即有1+b-2=0,且lna+b-2=-1,
解得,a=1,b=1;
则f(x)=lnx-x,(x>0),
f′(x)=
| 1 |
| x |
| 1-x |
| x |
当x>1时,f′(x)<0,f(x)递减,
当0<xx<1时,f′(x)>0,f(x)递增,
则有f(x)在x=1处取得极大值,也为最大值,且为f(1)=-1;
(Ⅱ)f(x)在(1,2)递减,f(x)的值域为(ln2-2,-1),
g(x)的导数为g′(x)=mx2-m=m(x2-1),
当m>0时,g′(x)>0在(1,2)成立,g(x)递增,g(x)的值域为(-
| 2 |
| 3 |
| 2 |
| 3 |
当m<0时,g′(x)<0在(1,2)成立,g(x)递减,g(x)的值域为(
| 2 |
| 3 |
| 2 |
| 3 |
任意x1∈(1,2),总存在x2∈(1,2),使f(x1)-g(x2)=0,
则在(1,2)内,当m>0时,(ln2-2,-1)⊆(-
| 2 |
| 3 |
| 2 |
| 3 |
即有-
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
当m>0时,(ln2-2,-1)⊆(
| 2 |
| 3 |
| 2 |
| 3 |
即有
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
则m的取值范围是(-∞,
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题考查导数的运用:求切线方程和求极值、最值,考查任意存在性问题注意转化为求函数的值域问题,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
设a,b∈R,则“(a-b)a2<0”是“a<b”的( )条件.
| A、充要 |
| B、充分而不必要 |
| C、必要而不充分 |
| D、既不充分也不必要 |
若集合A={x|
≤0},B={x|x≥-2}且A⊆B.则实数a的取值范围是( )
| x-a |
| x-2 |
| A、(-∞,-2] |
| B、[-2,2] |
| C、[-2,+∞) |
| D、[2,+∞) |
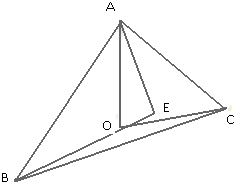 如图,O为△ABC的外心,E为三角形内一点,满足
如图,O为△ABC的外心,E为三角形内一点,满足