题目内容
若x,y满足
且z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、a∈(-4,0] |
| B、a∈[0,2) |
| C、a∈(-4,2) |
| D、a∈(-4,0)∪(0,2) |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用目标函数的意义,确定目标函数的斜率关系即可得到结论.
解答:
 解:画出区域图,可知当a=0时,z=2y,即y=
解:画出区域图,可知当a=0时,z=2y,即y=
z,符合题意;
当a>0时,y=-
x+
z,斜率-
>-1,即0<a<2时符合题意;
当a<0时,y=-
x+
z,斜率-
<2,即-4<a<0时符合题意;
综上,a∈(-4,2),
故选:C.
 解:画出区域图,可知当a=0时,z=2y,即y=
解:画出区域图,可知当a=0时,z=2y,即y=| 1 |
| 2 |
当a>0时,y=-
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
当a<0时,y=-
| a |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
综上,a∈(-4,2),
故选:C.
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键,要注意对a进行分类讨论.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
设p:x=3,q:x2-2x-3=0,则下面表述正确的是( )
| A、p是q的充分条件,但p不是q的必要条件 |
| B、p是q的必要条件,但p不是q的充分条件 |
| C、p是q的充要条件 |
| D、p既不是q的充分条件也不是q的必要条件 |
若函数f(x)=sin(2x+φ)满足f(x)≥f(
),则函数f(x)的单调递增区间是( )
| π |
| 3 |
A、[2kπ-
| ||||
B、[2kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
若向量
=(4,y)(y∈R),则“y=3”是“|
|=5”的( )
| a |
| a |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
将函数f(x)=x3+3x2+3x的图象按向量
平移后得到函数g(x)的图象,若函数g(x)满足g(1-x)+g(1+x)=1,则向量
的坐标是( )
| a |
| a |
| A、(-1,-1) | ||
B、(2,
| ||
| C、(2,2) | ||
D、(-2,-
|
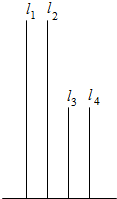
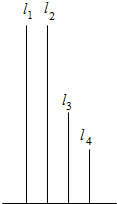
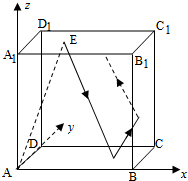 如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )
如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )