题目内容
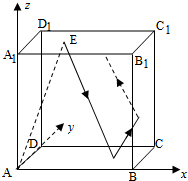 如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )
如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为li(i=2,3,4),l1=AE,将线段l1,l2,l3,l4竖直放置在同一水平线上,则大致的图形是( )A、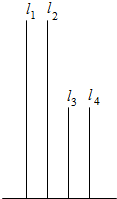 |
B、 |
C、 |
D、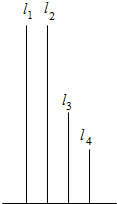 |
考点:真题集萃,空间中的点的坐标,点、线、面间的距离计算
专题:空间向量及应用
分析:根据平面反射定理,列出反射线与入射线的关系,得到入射线与反射平面的交点,再利用两点间的距离公式,求出距离,即可求解.
解答:
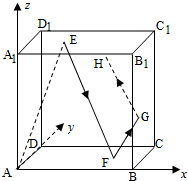 解:根据题意有:
解:根据题意有:
A的坐标为:(0,0,0),B的坐标为(11,0,0),C的坐标为(11,7,0),D的坐标为(0,7,0);
A1的坐标为:(0,0,12),B1的坐标为(11,0,12),C1的坐标为(11,7,12),D1的坐标为(0,7,12);
E的坐标为(4,3,12)
(1)l1长度计算
所以:l1=|AE|=
=13.
(2)l2长度计算
将平面A1B1C1D1沿Z轴正向平移AA1个单位,得到平面A2B2C2D2;显然有:
A2的坐标为:(0,0,24),B2的坐标为(11,0,24),C2的坐标为(11,7,24),D2的坐标为(0,7,24);
显然平面A2B2C2D2和平面ABCD关于平面A1B1C1D1对称.
设AE与的延长线与平面A2B2C2D2相交于:E2(xE2,yE2,24)
根据相似三角形易知:
xE2=2xE=2×4=8,
yE2=2yE=2×3=6,
即:E2(8,6,24)
根据坐标可知,E2在长方形A2B2C2D2内.
根据反射原理,E2在平面ABCD上的投影即为AE反射光与平面ABCD的交点.
所以F的坐标为(8,6,0).
因此:l2=|EF|=
=13.
(3)l3长度计算
设G的坐标为:(xG,yG,zG)
如果G落在平面BCC1B1;
这个时候有:xG=11,yG≤7,zG≤12
根据反射原理有:AE∥FG
于是:向量
与向量
共线;
即有:
=λ
因为:
=(4,3,12);
=(xG-8,yG-6,zG-0)=(3,yG-6,zG)
即有:(4,3,12)=λ(3,yG-6,zG)
解得:yG=
,zG=9;
故G的坐标为:(11,
,9)
因为:
>7,故G点不在平面BCC1B1上,
所以:G点只能在平面DCC1D1上;
因此有:yG=7;xG≤11,zG≤12
此时:
=(xG-8,yG-6,zG-0)=(xG-8,1,zG)
即有:(4,3,12)=λ(xG-8,1,zG)
解得:xG=
,zG=4;
满足:xG≤11,zG≤12
故G的坐标为:(
,7,4)
所以:l3=|FG|=
=
(4)l4长度计算
设G点在平面A1B1C1D1的投影为G’,坐标为(
,7,12)
因为光线经过反射后,还会在原来的平面内;
即:AEFGH共面
故EG的反射线GH只能与平面A1B1C1D1相交,且交点H只能在A1G';
易知:l4>|GG’|=12-4=8>l3.
根据以上解析,可知l1,l2,l3,l4要满足以下关系:
l1=l2;且l4>l3
对比ABCD选项,可知,只有C选项满足以上条件.
故本题选:C.
 解:根据题意有:
解:根据题意有:A的坐标为:(0,0,0),B的坐标为(11,0,0),C的坐标为(11,7,0),D的坐标为(0,7,0);
A1的坐标为:(0,0,12),B1的坐标为(11,0,12),C1的坐标为(11,7,12),D1的坐标为(0,7,12);
E的坐标为(4,3,12)
(1)l1长度计算
所以:l1=|AE|=
| (4-0)2+(3-0)2+(12-0)2 |
(2)l2长度计算
将平面A1B1C1D1沿Z轴正向平移AA1个单位,得到平面A2B2C2D2;显然有:
A2的坐标为:(0,0,24),B2的坐标为(11,0,24),C2的坐标为(11,7,24),D2的坐标为(0,7,24);
显然平面A2B2C2D2和平面ABCD关于平面A1B1C1D1对称.
设AE与的延长线与平面A2B2C2D2相交于:E2(xE2,yE2,24)
根据相似三角形易知:
xE2=2xE=2×4=8,
yE2=2yE=2×3=6,
即:E2(8,6,24)
根据坐标可知,E2在长方形A2B2C2D2内.
根据反射原理,E2在平面ABCD上的投影即为AE反射光与平面ABCD的交点.
所以F的坐标为(8,6,0).
因此:l2=|EF|=
| (8-4)2+(6-3)2+(0-12)2 |
(3)l3长度计算
设G的坐标为:(xG,yG,zG)
如果G落在平面BCC1B1;
这个时候有:xG=11,yG≤7,zG≤12
根据反射原理有:AE∥FG
于是:向量
| AE |
| FG |
即有:
| AE |
| FG |
因为:
| AE |
| FG |
即有:(4,3,12)=λ(3,yG-6,zG)
解得:yG=
| 33 |
| 4 |
故G的坐标为:(11,
| 33 |
| 4 |
因为:
| 33 |
| 4 |
所以:G点只能在平面DCC1D1上;
因此有:yG=7;xG≤11,zG≤12
此时:
| FG |
即有:(4,3,12)=λ(xG-8,1,zG)
解得:xG=
| 28 |
| 3 |
满足:xG≤11,zG≤12
故G的坐标为:(
| 28 |
| 3 |
所以:l3=|FG|=
(
|
| 13 |
| 3 |
(4)l4长度计算
设G点在平面A1B1C1D1的投影为G’,坐标为(
| 28 |
| 3 |
因为光线经过反射后,还会在原来的平面内;
即:AEFGH共面
故EG的反射线GH只能与平面A1B1C1D1相交,且交点H只能在A1G';
易知:l4>|GG’|=12-4=8>l3.
根据以上解析,可知l1,l2,l3,l4要满足以下关系:
l1=l2;且l4>l3
对比ABCD选项,可知,只有C选项满足以上条件.
故本题选:C.
点评:本题主要考察的空间中点坐标的概念,两点间的距离公式,解法灵活,属于难题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
已知数列{an}满足a1=2,an+1=
(n∈N*),则a2014=( )
| -1 |
| an+1 |
| A、2 | ||
B、-
| ||
C、-
| ||
D、
|
在0°~360°范围内,与-390°终边相同的角是( )
| A、30° | B、60° |
| C、210° | D、330° |
若x,y满足
且z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、a∈(-4,0] |
| B、a∈[0,2) |
| C、a∈(-4,2) |
| D、a∈(-4,0)∪(0,2) |
设sinθ=
(m>0),则cos(θ+
)的取值范围是( )
| m2+1 |
| 4m |
| π |
| 6 |
A、[-1,
| ||||||
B、[-1,
| ||||||
C、[-
| ||||||
D、[-
|