题目内容
若双曲线
-
=1(a>0,b>0)的右顶点与右焦点到双曲线渐近线的距离的和为
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3b |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:求出双曲线的右顶点以及右焦点,利用已知条件列出a、b、c关系式,然后求解离心率.
解答:
解:右顶点(a,0)到双曲线渐近线bx-ay=0的距离为:
=
.
右焦点(c,0)到双曲线渐近线bx-ay=0的距离为:b,
双曲线
-
=1(a>0,b>0)的右顶点与右焦点到双曲线渐近线的距离的和为
,
∴
+b=
,
解得离心率为e=
=2.
故选:C.
| |ab| | ||
|
| ab |
| c |
右焦点(c,0)到双曲线渐近线bx-ay=0的距离为:b,
双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| 3b |
| 2 |
∴
| ab |
| c |
| 3b |
| 2 |
解得离心率为e=
| c |
| a |
故选:C.
点评:本题考查双曲线的离心率的求法,点到直线的距离公式的应用,基本知识的考查.

练习册系列答案
相关题目
向量
=(cosα,sinα),
=(cosx,sinx),若函数f(x)=
•
是奇函数,则α可以是( )
| a |
| b |
| a |
| b |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
在0°~360°范围内,与-390°终边相同的角是( )
| A、30° | B、60° |
| C、210° | D、330° |
已知集合A={1,zi},B={2},i为虚数单位,若A∩B=B,则纯虚数z为( )
| A、-i | B、-2i | C、i | D、2i |
若x,y满足
且z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、a∈(-4,0] |
| B、a∈[0,2) |
| C、a∈(-4,2) |
| D、a∈(-4,0)∪(0,2) |
设sinθ=
(m>0),则cos(θ+
)的取值范围是( )
| m2+1 |
| 4m |
| π |
| 6 |
A、[-1,
| ||||||
B、[-1,
| ||||||
C、[-
| ||||||
D、[-
|
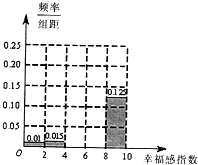 “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: