题目内容
△ABC的内角A,B,C所对的边分别为a,b,c,向量
=(2sin
,2
),
=(cosB,2cos2
-1),且
∥
.
(Ⅰ)求角B的余弦值;
(Ⅱ)若b=2,求S△ABC的最大值.
| m |
| B |
| 2 |
| 2 |
| n |
| B |
| 4 |
| m |
| n |
(Ⅰ)求角B的余弦值;
(Ⅱ)若b=2,求S△ABC的最大值.
考点:余弦定理的应用,平面向量的综合题
专题:解三角形,不等式的解法及应用
分析:(Ⅰ)利用向量平行的坐标公式,建立方程关系,即可求角B的余弦值;
(Ⅱ)根据余弦定理结合三角形的面积公式以及基本不等式的性质即可求出三角形面积的最值.
(Ⅱ)根据余弦定理结合三角形的面积公式以及基本不等式的性质即可求出三角形面积的最值.
解答:
解:(Ⅰ)∵向量
=(2sin
,2
),
=(cosB,2cos2
-1),且
∥
,
∴2sin
(2cos2
-1)-2
cosB=0;
即2sin
cos
=2
cosB,
则sinB=2
cosB,①
联立sin2B+cos2B=1,解得cosB=
.
(Ⅱ)在△ABC中,由余弦定理得b2=a2+c2-2accosB≥2ac-2accosB,
∵b=2,得cosB=
.
∴4≥2ac-2ac•
=
ac,即ac≤3当且仅当a=c取等号.
S△ABC=
ac•sinB=
ac•
=
×
ac=
ac≤
×3=
,
即S△ABC的面积的最大值为
.
| m |
| B |
| 2 |
| 2 |
| n |
| B |
| 4 |
| m |
| n |
∴2sin
| B |
| 2 |
| B |
| 4 |
| 2 |
即2sin
| B |
| 2 |
| B |
| 2 |
| 2 |
则sinB=2
| 2 |
联立sin2B+cos2B=1,解得cosB=
| 1 |
| 3 |
(Ⅱ)在△ABC中,由余弦定理得b2=a2+c2-2accosB≥2ac-2accosB,
∵b=2,得cosB=
| 1 |
| 3 |
∴4≥2ac-2ac•
| 1 |
| 3 |
| 4 |
| 3 |
S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1-cos2B |
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| 2 |
即S△ABC的面积的最大值为
| 2 |
点评:本题主要考查解三角形的应用,利用向量平行的坐标公式求出cosB是解决本题的关键,综合考查的余弦定理以及基本不等式的应用.综合性较强.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若x,y满足
且z=ax+2y仅在点(1,0)处取得最小值,则实数a的取值范围是( )
|
| A、a∈(-4,0] |
| B、a∈[0,2) |
| C、a∈(-4,2) |
| D、a∈(-4,0)∪(0,2) |
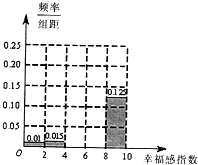 “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示:
“幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度时,给出的区间内的一个数,该数越接近10表示越满意,为了解某大城市市民的幸福感,随机对该城市的男、女各500人市民进行了调查,调查数据如下表所示: