题目内容
曲线 x2-y2=λ和曲线(x-1)2+y2=1有且仅有两个不同的公共点,则λ满足 .
考点:圆与圆锥曲线的综合
专题:计算题,圆锥曲线的定义、性质与方程
分析:曲线 x2-y2=λ和曲线(x-1)2+y2=1联立可得2x2-2x-λ>0,利用△>0可解答案.
解答:
解:曲线 x2-y2=λ和曲线(x-1)2+y2=1联立可得2x2-2x-λ>0,
∵曲线x2-y2=λ和曲线(x-1)2+y2=1有且仅有两个不同的公共点,
∴△=4+8λ>0且λ≠0,
∴λ>-
且λ≠0.
故答案为:λ>-
且λ≠0.
∵曲线x2-y2=λ和曲线(x-1)2+y2=1有且仅有两个不同的公共点,
∴△=4+8λ>0且λ≠0,
∴λ>-
| 1 |
| 2 |
故答案为:λ>-
| 1 |
| 2 |
点评:本题考查圆与圆锥曲线的综合,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
已知数列{an}的首项为a1=1,且满足对任意的n∈N*,都有an+1-an≤2n,an+2-an≥3×2n成立,则a2014=( )
| A、22014-1 |
| B、22014+1 |
| C、22015-1 |
| D、22015+1 |
已知
=(sinx,1,cox),
=(-1,sinx,cox)则
+
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
若|
|=|
|=|
•
|,则
与
+
的夹角为( )
| a |
| b |
| a |
| b |
| b |
| a |
| b |
| A、30° | B、60° |
| C、150° | D、120° |
已知椭圆
+y2=1和双曲线
-y2=1共焦点F1,F2,P为两曲线的一个公共点,则∠F1PF2的大小为( )
| x |
| m |
| x2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
“m=-1”是“直线mx+(2m-1)y+1=0和直线3x+my+2=0垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
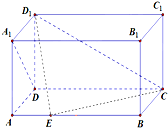 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=