��Ŀ����
��֪����f��x���Ķ�����Ϊ��0��+�ޣ�����y=
�ڣ�0��+�ޣ���Ϊ�����������f��x��Ϊ��һ�ױ�������������y=
�ڣ�0��+�ޣ���Ϊ�����������f��x��Ϊ�����ױ�����������
���ǰ����С�һ�ױ�����������ɵļ��ϼ�Ϊ��1�����С����ױ�����������ɵļ��ϼ�Ϊ��2��
��1����֪����f��x��=x3-2hx2-hx����f��x���ʦ�1��f��x��∉��2����ʵ��h��ȡֵ��Χ��
��2����֪0��a��b��c��f��x���ʦ�1��f��x���IJ��ֺ���ֵ���±���������֤��d��2d+t-4����0��
��3�����弯�Ϧ�={f��x��|f��x���ʦ�2���Ҵ��ڳ���k��ʹ����ȡx�ʣ�0��+�ޣ���f��x����k}�����ʣ��Ƿ���ڳ���M��ʹ��?f��x���ʦף�?x�ʣ�0��+�ޣ�����f��x����M�����������ڣ����M����Сֵ���������ڣ�˵�����ɣ�
| f(x) |
| x |
| f(x) |
| x2 |
���ǰ����С�һ�ױ�����������ɵļ��ϼ�Ϊ��1�����С����ױ�����������ɵļ��ϼ�Ϊ��2��
��1����֪����f��x��=x3-2hx2-hx����f��x���ʦ�1��f��x��∉��2����ʵ��h��ȡֵ��Χ��
��2����֪0��a��b��c��f��x���ʦ�1��f��x���IJ��ֺ���ֵ���±���������֤��d��2d+t-4����0��
| x | a | b | c | a+b+c |
| f��x�� | d | d | t | 4 |
���㣺���õ�����������Ϻ�������ֵ
ר�⣺�������ۺ�Ӧ��
��������1�����ݣ�f��x���ʦ�1��f��x��∉��2���ɵ�y=
=x2-2hx-h�����ö��κ����ĵ����Կɵ�-
=h��0����y=
=x-2h-
��y��=x+
����h�������ۿɵã���h��0����ʱf��x���ʦ�2����h��0ʱ��y��=
������
��x�ʣ�0��+�ޣ��м�ֵ�㣬�ɵ�f��x��∉��2�����ɵó���
��2����f��x���ʦ�1��ȡ0��x1��x2��x1+x2���ɵ�
��
��
���ɱ����֪��f��a��=d��f��b��=d��f��c��=t��f��a+b+c��=4��0��a��b��c��a+b+c�����á�һ�ױ����������ɵ�
��
��
��
�������ò���ʽ�����ʼ��ɵó���
��3�����ݡ����ױ�����������֤��f��x����0��x�ʣ�0��+�ޣ���������֤��f��x��=0�ڣ�0��+�ޣ����⣮���ɵó���
| f(x) |
| x |
| -2h |
| 2 |
| f(x) |
| x2 |
| h |
| x |
| h |
| x2 |
| x3+h |
| x2 |
| f(x) |
| x2 |
��2����f��x���ʦ�1��ȡ0��x1��x2��x1+x2���ɵ�
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(x1+x2) |
| x1+x2 |
| d |
| a |
| d |
| b |
| t |
| c |
| 4 |
| a+b+c |
��3�����ݡ����ױ�����������֤��f��x����0��x�ʣ�0��+�ޣ���������֤��f��x��=0�ڣ�0��+�ޣ����⣮���ɵó���
���
��1���⣺y=
=x2-2hx-h����f��x���ʦ�1����h��0��
y=
=x-2h-
��y��=x+
����h��0��x��0ʱ��y�䣾0����ʱf��x���ʦ�2�����������⣬��ȥ��
��h��0ʱ��y��=
����ʱ����
��x�ʣ�0��+�ޣ��м�ֵ�㣬���f��x��∉��2��
���Ͽɵã���h��0ʱ��f��x���ʦ�1��f��x��∉��2��
���h��ȡֵ��Χ�ǣ�-�ޣ�0����
��2��֤������f��x���ʦ�1����ȡ0��x1��x2��
��
��
��
��
�ɱ����֪��f��a��=d��f��b��=d��f��c��=t��f��a+b+c��=4��
��0��a��b��c��a+b+c��
��
��
��
��
��
��d��0��d��
��d��
��t��
��
��2d+t��4��
��d��2d+t-4����0��
�����ϺϦ�={f��x��|f��x���ʦ�2���Ҵ��ڳ���k��ʹ����ȡx�ʣ�0��+�ޣ���f��x����k}��
�����f��x���ʦף����ڳ���k��ʹ�� f��x����k ��x�ʣ�0��+�ޣ�������
������֤��f��x����0��x�ʣ�0��+�ޣ�������
�������x0�ʣ�0��+�ޣ���ʹ��f��x0����0��
��
=m��0
��f��x���Ƕ��ױ�����������
����������
�൱x��x0ʱ��
��
=m��0��
��f��x����mx2��
��һ�������ҵ�һ��x1��x0��ʹ��f��x1����mx12��k��
����f��x����k ��x�ʣ�0��+�ޣ�����ì�ܣ�
��f��x����0��x�ʣ�0��+�ޣ�������
�����f��x���ʦף�f��x����0��x�ʣ�0��+�ޣ�������
��������֤��f��x��=0�ڣ�0��+�ޣ����⣮
�������x2��0��ʹ��f��x2��=0��
��f��x���Ƕ�������������
����������
һ������x3��x2��0��ʹ
��
=0����������֤���Ľ��ì�ܣ�
��f��x��=0�ڣ�0��+�ޣ����⣮
���ϣ����ǵõ�����f��x���ʦף�f��x����0��x�ʣ�0��+�ޣ�������
����ڳ���M��0��ʹ�ô���f��x���ʦף�?x�ʣ�0��+�ޣ�����f��x����M������
����f��x��=-
��x��0������f��x����0��x�ʣ�0��+�ޣ�������
����
=-
�ڣ�0��+�ޣ�������������
��f��x���ʦף�
����ȡ����k��0���ܿ����ҵ�һ��xn��0��ʹ��x��xnʱ����f��x����k��
��M����Сֵ Ϊ0��
| f(x) |
| x |
y=
| f(x) |
| x2 |
| h |
| x |
| h |
| x2 |
��h��0ʱ��y��=
| x3+h |
| x2 |
| f(x) |
| x2 |
���Ͽɵã���h��0ʱ��f��x���ʦ�1��f��x��∉��2��
���h��ȡֵ��Χ�ǣ�-�ޣ�0����
��2��֤������f��x���ʦ�1����ȡ0��x1��x2��
��
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(x1+x2) |
| x1+x2 |
�ɱ����֪��f��a��=d��f��b��=d��f��c��=t��f��a+b+c��=4��
��0��a��b��c��a+b+c��
��
| d |
| a |
| d |
| b |
| t |
| c |
| 4 |
| a+b+c |
��d��0��d��
| 4a |
| a+b+c |
| 4b |
| a+b+c |
| 4a |
| a+b+c |
��2d+t��4��
��d��2d+t-4����0��
�����ϺϦ�={f��x��|f��x���ʦ�2���Ҵ��ڳ���k��ʹ����ȡx�ʣ�0��+�ޣ���f��x����k}��
�����f��x���ʦף����ڳ���k��ʹ�� f��x����k ��x�ʣ�0��+�ޣ�������
������֤��f��x����0��x�ʣ�0��+�ޣ�������
�������x0�ʣ�0��+�ޣ���ʹ��f��x0����0��
��
| f(x0) | ||
|
��f��x���Ƕ��ױ�����������
| f(x) |
| x2 |
�൱x��x0ʱ��
| f(x) |
| x2 |
| f(x0) | ||
|
��f��x����mx2��
��һ�������ҵ�һ��x1��x0��ʹ��f��x1����mx12��k��
����f��x����k ��x�ʣ�0��+�ޣ�����ì�ܣ�
��f��x����0��x�ʣ�0��+�ޣ�������
�����f��x���ʦף�f��x����0��x�ʣ�0��+�ޣ�������
��������֤��f��x��=0�ڣ�0��+�ޣ����⣮
�������x2��0��ʹ��f��x2��=0��
��f��x���Ƕ�������������
| f(x) |
| x2 |
һ������x3��x2��0��ʹ
| f(x3) | ||
|
| f(x2) | ||
|
��f��x��=0�ڣ�0��+�ޣ����⣮
���ϣ����ǵõ�����f��x���ʦף�f��x����0��x�ʣ�0��+�ޣ�������
����ڳ���M��0��ʹ�ô���f��x���ʦף�?x�ʣ�0��+�ޣ�����f��x����M������
����f��x��=-
| 1 |
| x |
����
| f(x) |
| x2 |
| 1 |
| x3 |
��f��x���ʦף�
����ȡ����k��0���ܿ����ҵ�һ��xn��0��ʹ��x��xnʱ����f��x����k��
��M����Сֵ Ϊ0��
���������⿼���˺����ĵ����ԡ������ļ������壬���յ�������ȷ�����������Ժ���ֵʱ�Ĵ��ⲽ���ǽ��Ĺؼ���������������������������������ѶȽϴ�

��ϰ��ϵ�д�
�����Ŀ
��֪����A={x|x2-x-2��0}��B={x||x|��1}����A�ɣ�∁RB��=��������
| A����1��2�� |
| B����1��2] |
| C��[1��2�� |
| D��[1��2] |
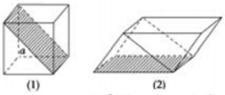 ��ͼ��1����ʾ����֪��������Խ��߳�Ϊa������Ӱ�潫���и�����飬ƴ����ͼ��2����ʾ�ļ����壬��ô�˼�����ı����Ϊ��������
��ͼ��1����ʾ����֪��������Խ��߳�Ϊa������Ӱ�潫���и�����飬ƴ����ͼ��2����ʾ�ļ����壬��ô�˼�����ı����Ϊ��������A����1+2
| ||
B����2+
| ||
C����3+2
| ||
D����4+
|
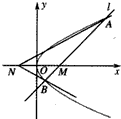 ��֪����M��a��0����a��0���Ķ�ֱ��l��������y2=4x��A��B���㣬��N���M����y��Գƣ�
��֪����M��a��0����a��0���Ķ�ֱ��l��������y2=4x��A��B���㣬��N���M����y��Գƣ�