题目内容
15.若y=tanωx在$(-\frac{π}{2},\frac{π}{2})$内为减函数,则( )| A. | ω≥1 | B. | ω≤-1 | C. | -1≤ω<0 | D. | 0<ω≤1 |
分析 利用正切函数的单调性,可得|ω|•$\frac{π}{2}$≤$\frac{π}{2}$,且ω<0,由此求得ω的范围.
解答 解:若y=tanωx在$(-\frac{π}{2},\frac{π}{2})$内为减函数,则|ω|•$\frac{π}{2}$≤$\frac{π}{2}$,且ω<0,求得-1≤ω<0,
故选:C.
点评 本题主要考查正切函数的单调性,属于基础题.

练习册系列答案
相关题目
5.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,四个顶点构成的四边形的面积为4,过原点的直线l(斜率不为零)与椭圆C交于A,B两点,F1,F2为椭圆的左、右焦点,则四边形AF1BF2的周长为( )
| A. | 4 | B. | $4\sqrt{3}$ | C. | 8 | D. | $8\sqrt{3}$ |
20.设正数x,y满足x2+$\frac{{y}^{2}}{2}$=1,则x•$\sqrt{1+{y}^{2}}$的最大值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{3\sqrt{2}}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3\sqrt{2}}{4}$ |
5.若数列{an}满足an=n,${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,则数列{bn}的前n项和Sn是( )
| A. | $\frac{n}{n+1}$ | B. | $\frac{2n}{n+1}$ | C. | $\frac{n-1}{n}$ | D. | $\frac{2n-2}{n}$ |
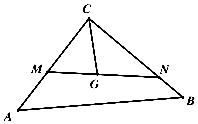 如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.
如图,等腰直角三角形ABC,点G是△ABC的重心,过点G作直线与CA,CB两边分别交于M,N两点,且$\overrightarrow{CM}=λ\overrightarrow{CA}$,$\overrightarrow{CN}=μ\overrightarrow{CB}$,则λ+4μ的最小值为3.


