题目内容
已知
=(2sin
,1),
=(cos
-
sin
,1),f(x)=
•
+m.
(1)求f(x)在[0,2π]上的单调区间;
(2)当x∈[0,2π]时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合;
(3)若存在实数a,b,c,使得a[f(x)-m]+b[f(x-c)-m]=1,对任意x∈R恒成立,求
的值.
| a |
| x |
| 2 |
| b |
| x |
| 2 |
| 3 |
| x |
| 2 |
| a |
| b |
(1)求f(x)在[0,2π]上的单调区间;
(2)当x∈[0,2π]时,f(x)的最小值为2,求f(x)≥2成立的x的取值集合;
(3)若存在实数a,b,c,使得a[f(x)-m]+b[f(x-c)-m]=1,对任意x∈R恒成立,求
| b |
| acosC |
考点:两角和与差的正弦函数,函数恒成立问题,平面向量数量积的运算,三角函数的最值
专题:三角函数的求值,三角函数的图像与性质
分析:(1)通过向量的数量积以及两角和与差的三角函数化简函数为一个角的一个三角函数的形式,通过正弦函数的单调区间求f(x)在[0,2π]上的单调区间;
(2)根据x∈[0,
],求得sin(x+
)min=
,可得f(x)min=2+m=2,由此求得m的值.再由f(x)≥2,可得2sin(x+
)+1≥2sin(x+
)≥
,2kπ+
≤x+
≤2kπ+
,由此求得x的集合.
(3)由题意可得对任意x∈R,(2a+2bcosc)sin(x+
)-2bsinccos(x+
)+b+a-1=0 恒成立,故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.由此求得
的值
(2)根据x∈[0,
| π |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
(3)由题意可得对任意x∈R,(2a+2bcosc)sin(x+
| π |
| 3 |
| π |
| 3 |
| b |
| acosC |
解答:
解:(1)
=(2sin
,1),
=(cos
-
sin
,1),
∴f(x)=
•
+m=sinx-2
sin2
+1+m
=sinx+
cosx+1-
+m
=2sin(x+
)+1-
+m
由2kπ-
≤x+
≤2kπ+
,k∈Z,
解得2kπ-
≤x≤2kπ+
,k∈Z,
f(x)在[0,2π]上的单调增区间:[0,
],[
,2π].
f(x)在[0,2π]上的单减调区间:[
,
];
(2)由于x∈[0,
],x+
∈[
,
],故sin(x+
)min=
,所以f(x)min=2+m=2,∴m=0.所以,f(x)=2sin(x+
)+1,由f(x)≥2,可得2sin(x+
)+1≥2sin(x+
)≥
,2kπ+
≤x+
≤2kπ+
,
∴{x|2kπ-
≤x≤2kπ+
k∈z}.
(3)∵a[f(x)-m]+b[f(x-C)-m]=a[2sin(x+
)+1]+b[2sin(x+
-C)+1]
=2asin(x+
)+a+2bsin(x+
)cosC-2bsinCcos(x+
)+b,
对任意x∈R,(2a+2bcosc)sin(x+
)-2bsinccos(x+
)+b+a-1=0 恒成立,
故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.
经讨论只能有 sinC=0,cosC=-1,a=b=
,所以,
cosC=-1.
| a |
| x |
| 2 |
| b |
| x |
| 2 |
| 3 |
| x |
| 2 |
∴f(x)=
| a |
| b |
| 3 |
| x |
| 2 |
=sinx+
| 3 |
| 3 |
=2sin(x+
| π |
| 3 |
| 3 |
由2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得2kπ-
| 5π |
| 6 |
| π |
| 6 |
f(x)在[0,2π]上的单调增区间:[0,
| π |
| 6 |
| 7π |
| 6 |
f(x)在[0,2π]上的单减调区间:[
| 7 |
| 6 |
| 7π |
| 6 |
(2)由于x∈[0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
∴{x|2kπ-
| π |
| 6 |
| π |
| 2 |
(3)∵a[f(x)-m]+b[f(x-C)-m]=a[2sin(x+
| π |
| 3 |
| π |
| 3 |
=2asin(x+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
对任意x∈R,(2a+2bcosc)sin(x+
| π |
| 3 |
| π |
| 3 |
故有(2a+2bcosC)=0,且2bsinC=0,且b+a-1=0.
经讨论只能有 sinC=0,cosC=-1,a=b=
| 1 |
| 2 |
| b |
| a |
点评:本题主要考查复合三角函数的单调性,两个向量的数量积的运算,函数的恒成立问题,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
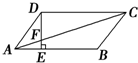 如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )
如图所示,在平行四边形ABCD中,AE:EB=1:2,若S△AEF=6cm2,则S△ADF为( )| A、54cm2 |
| B、24cm2 |
| C、18cm2 |
| D、12cm2 |
 如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设
如图所示,四棱柱ABCD-A1B1C1D1中,底面为平行四边形,以顶点A为端点的三条棱长都为1,且两两夹角为60°,设