题目内容

如图所示，四棱柱ABCD-A1B1C1D1中，底面为平行四边形，以顶点A为端点的三条棱长都为1，且两两夹角为60°，设
AB
=
a
，
AD
=
b
，
AA1
=
c
．
（1）求AC1的长；
（2）求BD1与AC所成角的余弦值．
考点：异面直线及其所成的角,空间向量的夹角与距离求解公式
专题：空间角
分析：（1）由
AC1
=
a
+
b
+
c
，利用向量法能求出AC1的长．
（2）由
BD
=
b
+
c
-
a
，
AC
=
a
+
b
，cos＜
BD1
，
AC
＞=
(
b
+
c
-
a
)•(
a
+
b
)
|
BD1
|•|
AC
|
，能求出BD1与AC所成角的余弦值．
解答： （1）解：由已知得，
a
•
b
=
1
2
，
b
•
c
=
1
2
，
a
•
c
=
1
2
，
|
a
|=|
b
|=|
c
|=1，…（3分）
又
AC1
=
a
+
b
+
c
，
∴|
AC
|=
(
a
+
b
+
c
)2
=
1+1+1+1+1+1
=
6
．（6分）
（2）解：∵
BD
=
b
+
c
-
a
，
AC
=
a
+
b
．…（8分）
∴cos＜
BD1
，
AC
＞=
(
b
+
c
-
a
)•(
a
+
b
)
|
BD1
|•|
AC
|

=
1
2
+1+
1
2
+
1
2
-1-
1
2
2
•
3

=
6
6
． …（12分）
点评：本题考查线段长的求法，考查两条异面直线所成角的余弦值的求法，是中档题，解题时要注意向量法的合理运用．
练习册系列答案
相关题目
已知（1+mx）n（m∈R，n∈N*）的展开式的二项式系数之和为32，且展开式中含x3项的系数为80．
（1）求m，n的值；
（2）求（1+mx）n（1-x）6展开式中含x2项的系数．
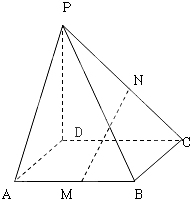在四棱锥P-ABCD中，PD⊥平面ABCD，底面是边长是1的正方形，M，N分别是AB，PC的中点；
（1）求证：MN∥平面PAD；
（2）求证：BC⊥平面PCD．
已知向量
a
=（3，-4tanα），
b
=（4，5cosα）．
（1）若
a
∥
b
，求sinα的值；
（2）若
a
⊥
b
，且α∈（0，
π
2
），求cos（2α-
π
3
）的值．
已知
a
=（2sin
x
2
，1），
b
=（cos
x
2
-
3
sin
x
2
，1），f（x）=
a
•
b
+m．
（1）求f（x）在[0，2π]上的单调区间；
（2）当x∈[0，2π]时，f（x）的最小值为2，求f（x）≥2成立的x的取值集合；
（3）若存在实数a，b，c，使得a[f（x）-m]+b[f（x-c）-m]=1，对任意x∈R恒成立，求
b
acosC
的值．
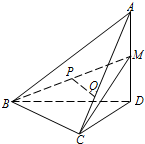如图，在四面体A-BCD中，AD⊥平面BCD，BC⊥CD，AD=2，BD=2
2
．M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ=3QC．
（1）证明：PQ∥平面BCD；
（2）若∠BDC=45°，求直线BM与平面ABC所成角的余弦值．
长方体ABCD-A1B1C1D1中，AB=BC=2a，AA1=a，E，F分别是A1B1和BB1的中点，求EF与AD1所成角的余弦值．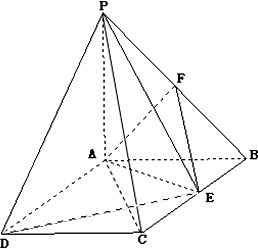
如图：PA⊥平面ABCD，ABCD是矩形，PA=AB=1，点E，F分别是BC，PB的中点．
（Ⅰ）证明：EF∥平面PAC；
（Ⅱ）当AD等于何值时，二面角P-DE-A的大小为30°．
已知y=lg（ax-1）-lg（x-1）在（10，+∞）上是增函数，则a的取值范围
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网